Теоретическая механика. Часть II: Кинематика: Методические указания и контрольные задания, страница 7

Предположим, что вектор  направлен вверх. Проведя перпендикуляры к векторам  и  из точек А и В, найдём точку их пересечения Е. Эта точка будет являться мгновенным центром скоростей шатуна АВ. Из треугольника АВЕ определим

Из треугольника АСЕ по теореме косинусов

Шатун АВ совершает поступательное движение, которое можно заменить вращательным движением вокруг МЦС (точки Е).

Угловая скорость поворота шатуна

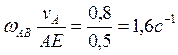
 направлена в ту сторону, куда указывает  относительно точки Е.

Во вращательном движении шатуна точки В и С имеют линейные скорости

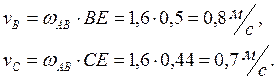
Векторы  и  направлены перпендикулярно их расстояниям до МЦС – ВЕ и СЕ соответственно в ту сторону, куда указывает .  Таким образом, направление  указано верно.

2) Определение ускорений точек

Участвуя в движении кривошипа ОА, точка А имеет ускорение, которое складывается из двух составляющих:

                (1)

где  - нормальное ускорение точки А,

 - тангенциальное ускорение точки А.

Нормальное ускорение точки А

Вектор  направлен от точки А к точке О

Тангенциальное ускорение точки А

Вектор  направлен перпендикулярно АО в ту сторону, куда указывает .

Точка В принадлежит одновременно шатуну АВ и коромыслу ВО₂:

Участвуя в движении коромысла ВО₂ (вращательном), точка В имеет ускорение, которое складывается из двух составляющих

                (2)

где  - нормальное ускорение точки В,

 - тангенциальное ускорение точки В.

Нормальное ускорение точки В

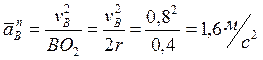
Вектор  направлен от точки В к точке О₂

Тангенциальное ускорение точки В

 величина неизвестная, т.к.  не задано.

Вектор  направлен перпендикулярно ВО₂ (направление указываем произвольно)

Участвуя с шатуном АВ в плоскопараллельном движении, точка В имеет ускорение, определить которое можно, приняв за полюс точку А.

               (3)

где  - ускорение, которое имеет точка В во вращательном движении шатуна АВ относительно точки А (полюса). Это ускорение складывается из двух составляющих

            (4)

где  - нормальное ускорение точки В при повороте шатуна относительно полюса А

 - тангенциальное ускорение точки В в этом движении

Нормальное ускорение

Вектор  направлен от точки В к полюсу (точке А)

Тангенциальное ускорение

               неизвестно, т.к.  не задано.

Вектор  направляем перпендикулярно АВ (направление указываем предположительно)

Подставляем (1), (4) в (3), получаем

                      (5)

Приравняем правые части (2) и (5), поскольку левые части в этих равенствах одинаковы

                        (6)

Решим уравнение (6), спроецировав его на прямую АВ (ось х):

, откуда

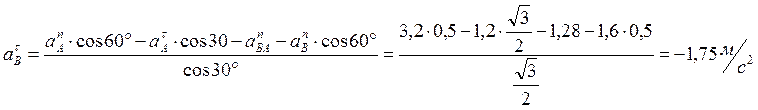
Используя равенство (2) и учитывая угол между векторами  и , воспользуемся теоремой Пифагора

Для определения углового ускорения шатуна  спроецируем равенство (6) на ось у:

 откуда

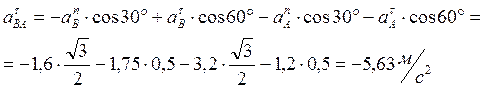
Знак показывает, что вектор  направлен противоположно направлению, указанному на схеме. Таким образом, угловое ускорение шатуна направлено по ходу часовой стрелки.

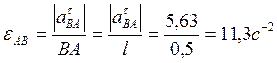
Для определения ускорения точки С составим аналогичное (5) равенство:

,                   (7)

где  - нормальное ускорение точки С при повороте шатуна относительно полюса А,

 - тангенциальное ускорение точки С в этом движении

Нормальное ускорение

Вектор  направлен от точки С к полюсу А

Тангенциальное ускорение

Вектор  направлен перпендикулярно СА в ту сторону, куда указывает

Спроецируем равенство (7) на оси х и у:

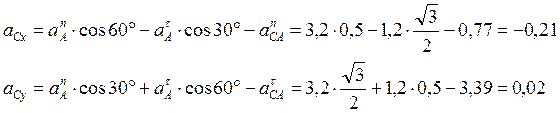
и определим ускорение точки С по её проекциям

Ответ:   

 

Задание №4

Определение абсолютной скорости и абсолютного ускорения точки.

Точка М движется по вращающейся пластине. По заданным уравнениям движения точки относительно пластины и её вращательного движения. Определить абсолютную скорость и абсолютное ускорение точки в заданное время . Номер схемы по рисунку и данные для расчёта выбрать из таблицы 4, согласно шифра. Положение точки М на схеме определяет положительное направление отсчёта на относительной траектории с началом отсчёта в точке А. Смещение оси вращения от центра пластины