Электротехника \ Теоретические основы электротехники

Определение выражения напряжения резистора в схеме RL-цепи первого порядка после коммутации

Страницы работы

6 страниц (Word-файл)

Скачать файл

Содержание работы

Классический анализ переходных процессов в RL-цепях

первого порядка

Задача 6.4

Рис. 6.1

Определите выражение напряжения u₅(t) резистора R₅ в схеме цепи Рис. 6.1 после коммутации и постройте его график, если

А, R₂ = R₃ = R₅ = 100 Ом, C₁ = 10 мкФ, L₄ = 100 мГн.

Решение.

Рис. 6.2

Совместим момент коммутации в цепи Рис. 6.1 с началом отсчёта относительного времени t в ней, то есть с моментом времени t = 0, когда

А, .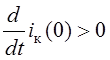

Предположим, что цепь до коммутации (t < 0) находилась в гармоническом процессе. Из комплексной схемы цепи до коммутации (Рис. 6.2) находим сначала комплексную амплитуду тока катушки I_m₄:

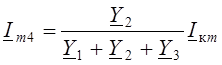где Y₁, Y₂ и Y₃ – комплексные проводимости ветвей схемы

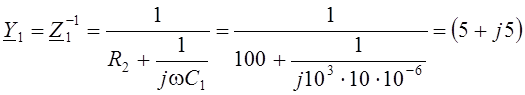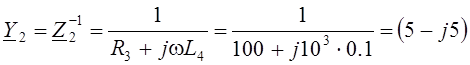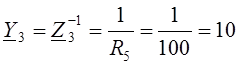мСм;

I_к_m – комплексная амплитуда задающего тока

А.

Тогда

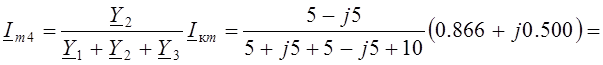
= А.

Запишем далее выражение мгновенного тока катушки i₄(t) до коммутации (t < 0)

А.

И, наконец, вычислим его значение к моменту коммутации (t = 0–)

– начальное значение тока катушки.


a)	b
Рис. 6.3

Составим теперь уравнение заданной цепи после коммутации (Рис. 6.3, a) для переменной её состояния – тока катушки i₄(t). Считая известным его мгновенное значение и опираясь на принцип компенсации *, изобразим схему замещения цепи для произвольного момента времени t ³ 0. (Рис. 6.3, b). Из этой схемы находим выражение напряжения катушки u₄(t):

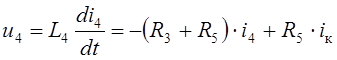
Обратите внимание на то, что множительпри i₂ представляет собой взятое со знаком минус выражение сопротивления пассивного двухполюсника (“освобождённого” от источника тока i_к(t)) относительно полюсов катушки.

Сокращая последнее выражение на L₄, получаем искомое уравнение состояния цепи, записанное в нормальной форме (форме Коши):

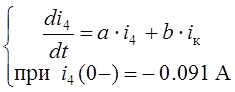Здесь

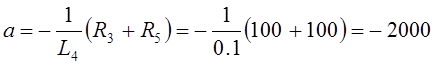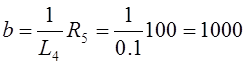с^-1;

с^-1.

Интегрируя его в пределах от 0– до 0+, получаем соотношение между начальным i₄(0–) и стартовым i₄(0+) значениями тока катушки, известное в теории цепей как первый закон коммутации:

i₄(0+) = i₄(0–) = –0.091 А.

Далее задачу решаем в два этапа. Сначала получим выражение переменной состояния (независимой переменной) цепи i₄(t) при t ³ 0 – тока катушки L₄ после размыкания ключа, а затем для тех же моментов времени t найдём выражение искомой зависимой переменной – напряжения u₅(t) резистора R₅ цепи Рис. 6.3.

I этап. При t ³ 0 ток катушки представим суммой двух составляющих

где i_4пр(t) – принуждённая составляющая тока катушки, совпадающая с его гармонической составляющей; i_4св(t) – свободная составляющая тока катушки.

Рис. 6.4

Из комплексной схемы цепи после коммутации (Рис. 6.4) находим сначала комплексную амплитуду I_m₄ принуждённой составляющей тока катушки i₄_пр(t):

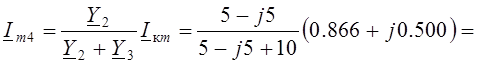
= А.

Запишем теперь выражение принуждённой составляющей тока катушки i₄(t) (t ³ 0)

А.

Для составления выражения свободной составляющей тока катушки получим сначала характеристическое уравнение и найдём его корни. Обращаясь к уравнению состояния цепи, записываем его характеристическое уравнение

a – p = 0,

единственный корень которого равен

p = a = – 2000 с^-1.

Отметим попутно, что значение постоянной времени t рассматриваемой цепи равно

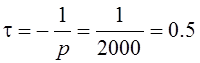мс .

При единственном корне характеристического уравнения

i_4св(t) = i_4св(0+) e^pt А.

В соответствии с принятым представлением при t ³ 0 ток катушки

i₄(t) = i_4пр(t) + i_4св(0+) e^pt А.

Полагая здесь t = 0+, находим

i_4св(0+) = i_4пр(0+) – i₄(0+) = – 0.091 – 0.447sin(0.06) = – 0.118 А.

Следовательно, ток катушки i₄(t) в цепи после коммутации (Рис. 6.3, a) представляется выражением:

i₄(t) = i_4пр(t) + i_4св(t) e^pt = i_4пр(t) + i_4св(0+) e^pt =

= 0.447sin(1000t + 0.06) – 0.118 e^{– 2000t} А при t ³ 0.

II этап. Выражение напряжения u₅(t) резистора R₅ в цепи после коммутации (Рис. 6.3, a) получим по её схеме замещения (Рис. 6.3, b), в которой на основании принципа компенсации катушка заменена источником найденного тока i₄(t):