Определение выражения напряжения резистора в схеме RL-цепи первого порядка после коммутации, страница 2

 В.

Свернём выражение принуждённой составляющей напряжения резистора u₅(t):

= 63.2sin(wt + 0.846) В.

Следовательно,

u₅(t) = 63.2sin(wt + 0.846) + 11.8 e^{– 2000t} В.

Примечание: Искомое выражение напряжения резистора u₅(t) при t ³ 0 также можно представить разложением

,

Выражение принуждённой составляющей напряжения u₅(t) проще было найти ещё на первом этапе анализа переходного процесса по схеме Рис. 6.4:

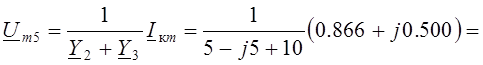
= 41.94 + j47.34 = 63.25 e ^j0.846 В.

a)	b
Рис. 6.5

u_5пр(t) = 63.2sin(wt + 0.846) В.

Выражение же свободной составляющей напряжения u₅(t) можно определить на втором этапе из анализа схемы замещения цепи, “освобождённой” от источника тока i_к(t) * (Рис. 6.5):

 В.

Зависимости напряжения u₅(t) и его компонентов на интервале времени 0 £ t £ 2 мс с шагом 0.25 мс представлены таблицей; Рис. 6.6 отображает их на интервале 0 £ t £ 5 мс.

Таблица

t, мс	0.0	0.25	0.50	0.75	1.00	1.25	1.50	1.75	2.00
u5пр(t), В	47.3	56.2	61.6	63.2	60.8	54.7	45.1	32.8	18.4
u5св(t), В	11.8	7.2	4.3	2.6	1.6	1.0	0.6	0.4	0.2
u5(t),   В	59.1	63.4	65.9	65.8	62.4	55.7	45.7	33.2	18.6

Примечание. В RL-цепях после коммутации с гармоническими задающими напряжениями или/и токами часто предпочтительнее сразу вычислять выражение искомой величины, не определяя предварительно выражение переменной состояния цепи. В таких случаях стартовое значение искомой величины находится из схемы цепи при t = 0+, в которой катушка заменяется источником стартового значения её тока.

Численное решение этой задачи осуществляется также в указанные два этапа.

Обратимся сначала к полученному ранее уравнению для переменной состояния цепи в виде

,

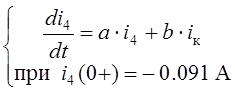в котором

        a = – 2000 с^-1,     b = 1000 См/с.

Численное решение уравнения для переменной состояния цепи i₄(t) при 0 £ t£ 5 мс найдём с помощью функции rkfixed математического пакета MathCad 7 Pro, реализующей метод Рунге-Кутта с фиксированным шагом. Для этого задаём последовательно:

                                – стартовое значение переменной состояния цепи i₄(0+);

             –  выражение её первой производной;

   – вычисление значений переменной состояния цепи i₄(t) в пятистах точках (500) интервала времени [0,0.005] с;

                       – номера точек разбиения интервала времени пробегают значения от 0 до числа строк без 1 матрицы Z.

                                        – элементам вектора t присваивают значения элементов первого столбца матрицы Z.

                                       – элементам вектора i₄ присваивают значения элементов второго столбца матрицы Z.

Выражение искомой зависимой переменной u₅(t) есть линейная функция переменной состояния i₄(t) и задающего тока i_к(t):

 В,

где                   с = – R₅ = – 100 Ом,              d = R₅ = 100 Ом.

Соответствующее выражение в протоколе MathCad 7 Pro выглядит так:

Результаты численного и аналитического исследования переходного процесса в рассматриваемой цепи полностью совпадают, по крайней мере до трёх цифр после запятой мантиссы мгновенных значений напряжения u₅(t).

C:\ОТЦиС\Упражнения\Тема_6a\Примеры_6a\Пример 4