







Классический анализ переходных процессов в RC-цепях
второго порядка
Задача 6.4
|
Рис. 6.1 |
Запишите выражение тока i1(t) конденсатора C1 в схеме цепи Рис. 6.1 после коммутации и
постройте их графики, если |
Решение.
Совместим момент коммутации ключа в цепи Рис. 6.1 с началом отсчёта относительного времени t в ней, то есть с моментом времени t = 0, когда
![]() В,
В, 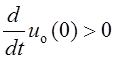 .
.
В качестве переменных состояния (независимых переменных) цепи после коммутации ключа (при t ³ 0) выберем напряжения конденсаторов u1(t) и u3(t). По умолчанию считается, что цепь накануне коммутации (t < 0) находится в гармоническом процессе. Из схем цепей Рис. 6.2, эквивалентных исходной схеме Рис. 6.1, вычислим значения напряжений u1(0–) и u3(0–) конденсаторов C1 и C3 к моменту коммутации – их начальные значения.
|
|
|
|
a) |
b) |
|
Рис. 6.2 |
|
Из схемы цепи до коммутации в стационарном состоянии (Рис. 6.3, a) находим начальное значение напряжения u1(0–) конденсатора C1 (*)
u1(0–) = 0 В.
Из комплексной схемы замещения (Рис. 6.3, b) второго фрагмента исходной схемы (Рис. 6.2, b) вычислим сначала значение комплексной амплитуды напряжения Um3 конденсатора C3:
|
|
|
|
a) |
b) |
|
Рис. 6.3 |
|
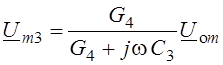 ,
,
где – G4 проводимость резистора R4
![]() См;
См;
jwC3 – комплексная проводимость конденсатора C3:
![]() См;
См;
Uom – комплексная амплитуда задающего напряжения
![]() В.
В.
Тогда
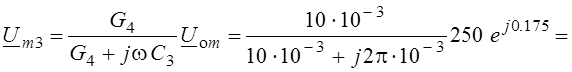
![]() В.
В.
Запишем далее выражение мгновенного напряжения конденсатора u3(t) до коммутации (t < 0)
![]() В.
В.
И, наконец, вычислим его значение к моменту коммутации
![]() В.
В.
– начальное значение напряжения конденсатора C3.
|
|
|
|
a) |
b) |
|
Рис. 6.4 |
|
Составим теперь систему дифференциальных уравнений для переменных состояния цепи после коммутации u1(t) и u3(t) (Рис. 6.4, a). Считая известными выражения их мгновенных значений и опираясь на известный принцип компенсации (*), изобразим схему замещения цепи для произвольного момента времени t ³ 0 (Рис. 6.4, b). Из этой схемы находим выражения токов i1(t) и i3(t) конденсаторов C1 и C3:
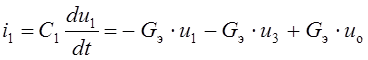 ,
,
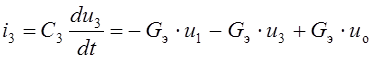 ,
,
где
![]() См.
См.
Сокращая первое из этих выражений на C1, а второе – на C3, получаем искомую систему уравнений состояния цепи, записанную в нормальной форме (форме Коши):
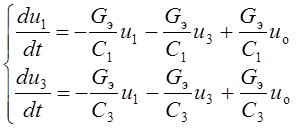
или
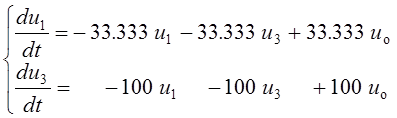
при u1(0–) = 0 В,
u3(0–) = – 79.692 В.
Интегрируя их в пределах от 0– до 0+, получаем соотношения между начальными u1(0–), u3(0–) и стартовыми u1(0+), u3(0+) значениями напряжений конденсаторов, известные в теории как выражение второго закона коммутации:
u1(0+) = u1(0–) = 0 В,
u3(0+) = u3(0–) = – 79.69 В.
Далее задачу решаем в два этапа. Сначала получим выражения переменных состояния (независимых переменных) цепи при t ³ 0 – напряжений конденсаторов u1(t) и u3(t) после замыкания ключа, а затем для тех же моментов времени t получим выражение искомой зависимой переменной – тока i1(t) конденсатора C1 цепи Рис. 6.4..
I этап. При t ³ 0 выражение напряжения каждого конденсатора представим суммой двух составляющих
![]() ,
,
![]() .
.
где u1пр(t) и u3пр(t) – выражения принуждённых составляющих напряжений конденсаторов, совпадающих с их гармоническими составляющими; u1ñâ(t) и u3св(t) – выражения свободных составляющих этих величин, представляющие собой общее решение системы дифференциальных уравнений состояния цепи.
Из комплексной схемы цепи после коммутации (Рис. 6.5) находим сначала значения комплексных амплитуд Um1 и Um3 принуждённых составляющих напряжений u1пр(t) и u3пр(t) конденсаторов C1 и C3. Обозначим
|
Рис. 6.5 |
Rэ = R2 + R4 = 400 + 100 = 500 Ом,
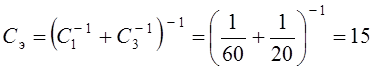 мкФ
мкФ
Тогда
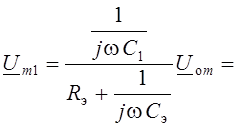 ,
,
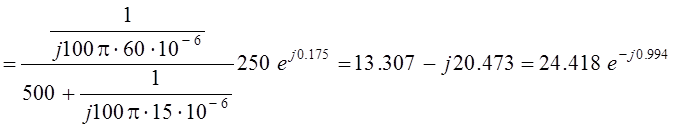 В;
В;
Очевидно
![]() В.
В.
Запишем теперь выражения принуждённых составляющих напряжений конденсаторов u1пр(t) и u3пр(t) (t ³ 0)
![]() В,
В,
![]() В.
В.
Здесь же найдём выражение принуждённой составляющей тока i1пр(t) конденсатора C1:
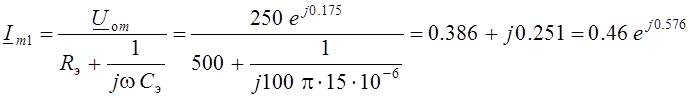 А;
А;
![]() А.
А.
Общее решение системы уравнений состояния цепи есть решение однородной системы дифференциальных уравнений
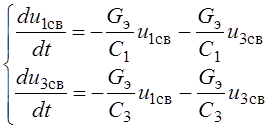 ,
,
которую можно записать в виде матричного дифференциального уравнения
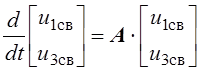 ,
,
где 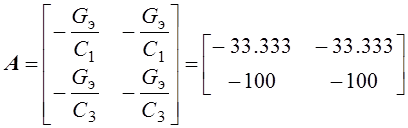 с–1.
с–1.
Составим характеристическое уравнение матрицы A однородной системы дифференциальных уравнений, оно же характеристическое уравнение цепи:
![]() ,
,
которое представляет собой условие существования нетривиального решения векторного уравнения (здесь E – единичная матрица). Перепишем его подробно
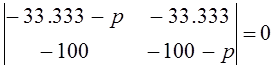 ;
;
раскроем
определитель, получим уравнение ![]() . Его корни p1
= 0 и p2 = – 133.33 с–1 –
характеристические числа матрицы A.
. Его корни p1
= 0 и p2 = – 133.33 с–1 –
характеристические числа матрицы A.
Проверка. Произведение корней характеристического уравнения равно значению определителя матрицы A, которое, в свою очередь, равно значению свободного члена характеристического уравнения:
![]() .
.
Вычислим теперь значения собственных векторов матрицы A системы дифференциальных уравнений, соответствующие найденным значениям характеристических чисел.
Найдём собственный вектор матрицы A,
отвечающий её собственному числу (значению) ![]() . Пусть
. Пусть
![]() ,
,
![]() .
.
Составим систему уравнений для определения V11 и V21:
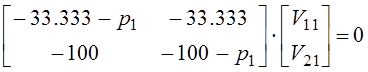
или
![]() ,
,
![]() .
.
Полагая ![]() , находим
, находим ![]() или собственный вектор
или собственный вектор
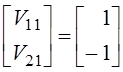 .
.
Найдём собственный вектор матрицы A,
отвечающий её собственному числу (значению) ![]() с–1. Пусть
с–1. Пусть
![]() ,
,
![]() .
.
Составим систему уравнений для определения V12 и V22:
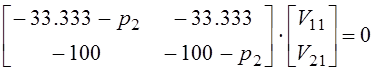
или
![]() ,
,
![]()
Полагая ![]() , находим
, находим ![]() или собственный вектор
или собственный вектор
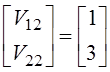 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.