Общее решение системы уравнений состояния цепи имеет вид
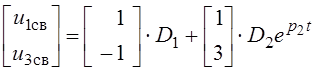
или в координатной форме
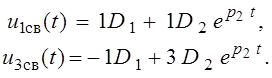
Отсюда видно, что значение постоянной времени t рассматриваемой цепи равно
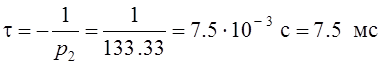 .
.
В соответствии с принятым представлением при t ³ 0 выражения напряжений конденсаторов u1(t) и u3(t)
![]() В,
В,
![]() В.
В.
Значения постоянных интегрирования D1 и D2 находятся по стартовым значениям искомых величин u1(0+) = 0 В, u3(0+) = – 79.69 В. Полагая здесь t = 0+, получаем неоднородную систему линейных алгебраических уравнений
![]() ,
,
![]() ,
,
или
![]() ,
,
![]() ,
,
где
u1св(0+) = u1(0+) – u1пр(0+) = 0 – 24.4sin(– 0.994) = 20.47 В,
u3св(0+) = u3(0+) – u3пр(0+) = – 79.69 – 73.2sin(– 0.994) = – 18.27 В.
Отсюда
D1 = 19.923 В, D2 = 0.550 В.
Запишем теперь окончательные выражения напряжений u1(t) и u3(t) конденсаторов C1 и C3 в цепи после коммутации (см. Таблицу и Рис. 6.4, a) (t ³ 0). В соответствие с принятым разложением:
![]() В,
В,
![]() В.
В.
Значения постоянных интегрирования можно также найти по стартовым значениям переменных состояния цепи и их первых производных (см. Приложение).
|
Рис. 6.6 |
Интересно отметить, что установившиеся напряжения конденсаторов представляются периодическими, но несинусоидальными функциями времени t
![]() В и
В и ![]() В,
В,
поскольку кроме гармонических содержат также постоянные составляющие (Рис. 6.6).
Проверка: Значения u1(0+) = 8.13×10-4 В и u3(0+) = – 79.67 В с точностью до трёх значащих цифр совпадают с известными стартовыми значениями этих величин.
II этап. Выражение тока i1(t) конденсатора C1 в цепи после коммутации (Рис. 6.4, a) можно получить по её схеме замещения (Рис. 6.4, b), в которой на основании принципа компенсации конденсаторы заменены источниками найденных напряжений u1(t) и u3(t):
![]() .
.
Но проще поступить иначе. Искомое выражение тока конденсатора i1(t) при t ³ 0 также можно представить разложением
![]() .
.
|
|
|
|
a) |
b |
|
Рис. 6.7 |
|
Выражение принуждённой составляющей i1пр(t) этого тока было получено ещё на первом этапе анализа переходного процесса.
Выражение же его свободной составляющей i1св(t) легко определить из анализа схемы замещения цепи после коммутации, “освобождённой” от источника напряжения uo(t) (*) (Рис. 6.7):
![]()
![]()
![]() А.
А.
Следовательно
![]() А.
А.
Проверка:
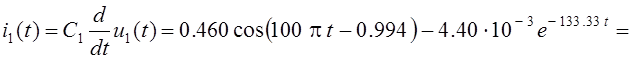
![]() А.
А.
Зависимость тока i1(t) на интервале 0 £ t £ 30 мс с шагом 3 мс представлены Таблицей и Рис. 6.6.
Таблица
|
t, мс |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
u1(t), В |
0 |
19.0 |
39.2 |
43.7 |
28.8 |
6.7 |
- 4.4 |
4.6 |
26.3 |
42.7 |
40.4 |
|
u3t), В |
-79.7 |
-22.6 |
37.8 |
51.3 |
6.6 |
-59.6 |
-92.9 |
-65.9 |
- 0.8 |
48.5 |
41.5 |
|
i1(t), мА |
247 |
457 |
287 |
- 121 |
- 431 |
- 386 |
- 24 |
358 |
444 |
164 |
- 252 |
Численное решение этой задачи осуществляется в те же два этапа.
Обратимся сначала к полученным ранее уравнениям для переменных состояния цепи в виде
Обратимся сначала к полученным ранее уравнениям для переменных состояния цепи в виде
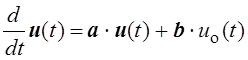 .
.
Здесь
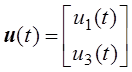 при
при 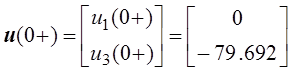 В;
В;
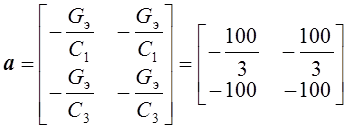 с-1,
с-1, 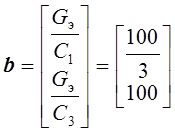 с-1.
с-1.
Численное решение уравнения для переменной состояния цепи при 0 £ t £ 30 мс найдём с помощью функции rkfixed математического пакета MathCad 2000 Pro, реализующей метод Рунге-Кутта с фиксированным шагом. После ввода исходных данных задачи устанавливаем значение ORIGIN = 0 и задаём последовательно:
|
|
– матрица коэффициентов однородной системы дифференциальных уравнений состояния цепи; |
|
|
– матрица коэффициентов правой части неоднородной системы дифференциальных уравнений состояния цепи; |
|
|
– стартовые значения u(0+) элементов вектора переменных состояния цепи u(t); |
![]() –
выражение первой производной вектора переменных состояния цепи u(t);
–
выражение первой производной вектора переменных состояния цепи u(t);
![]() –
вычисление значений вектора переменных состояния цепи u(t) в
шестистах точках (600) интервала времени [0,0.03] с;
–
вычисление значений вектора переменных состояния цепи u(t) в
шестистах точках (600) интервала времени [0,0.03] с;
![]() –
номера точек разбиения интервала времени [0,0.03] с
пробегают значения от 0 до числа строк без 1 матрицы Z.
–
номера точек разбиения интервала времени [0,0.03] с
пробегают значения от 0 до числа строк без 1 матрицы Z.
![]() –
элементам вектора t
присваивают значения элементов первого
столбца матрицы Z.
–
элементам вектора t
присваивают значения элементов первого
столбца матрицы Z.
![]() –
элементам вектора u1 присваивают значения
элементов второго столбца
матрицы Z.
–
элементам вектора u1 присваивают значения
элементов второго столбца
матрицы Z.
![]() – элементам вектора
u3
присваивают значения элементов третьего столбца матрицы Z.
– элементам вектора
u3
присваивают значения элементов третьего столбца матрицы Z.
Выражение искомой зависимой переменной i1(t) есть линейная функция переменных состояния u1(t), u3(t) и задающего напряжения uo(t):
![]() А,
А,
Соответствующее выражение в протоколе MathCad 2000 Pro выглядит так:
![]() .
.
Результаты численного и аналитического исследования переходного процесса в рассматриваемой цепи на интервале 0 £ t£ 30 мс полностью совпадают, по крайней мере до трёх цифр мантиссы мгновенных значений тока i1(t).
D:\ОТЦиС\Упражнения\Тема_6c\Примеры_6c\Пример 4
* Напомним, что конденсатор в стационарном состоянии эквивалентен разъёму.
* Любой элемент с известным значением напряжения может быть эквивалентно заменён источником напряжения известного значения.
* При uo(t) = 0 источник напряжения эквивалентен проводу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.