Дано:
Критерий
![]() ,
(1)
,
(1)
Дифференциальное уравнение
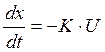 , (2)
, (2)
Ограничения
![]() . (3)
. (3)
Задание: используя принцип
максимума Понтрягина необходимо за конечное время ![]() перевести
объект из начального состояния с координатами
перевести
объект из начального состояния с координатами
![]() ;
; ![]() ;
; ![]() ;
; ![]() (4)
(4)
в конечное состояние таким образом, чтобы затраченная энергия управляющим устройством на этот перевод была минимальной, т.е. необходимо минимизировать функционал
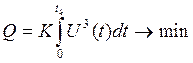 . (5)
. (5)
Ход работы:
Преобразуем дифференциальное уравнение (2) и выведем передаточную функцию линейного объекта первого порядка
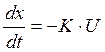 ,
,
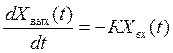 , (6)
, (6)
![]() ,
,
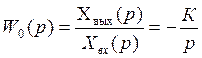 .
(7)
.
(7)
Обозначим
![]() ,
,
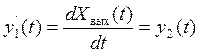 ,
,
![]() .
.
С учетом введенных обозначений составим систему линейных дифференциальных уравнений первого порядка
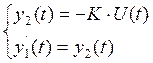 (8)
(8)
Полученную систему уравнений дополняем еще одним уравнением
![]() .
.
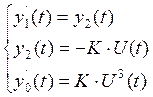
Составляем функцию Гамильтона
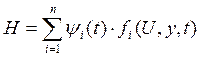 , (9)
, (9)
где
![]()
![]() ,
,
где ![]() - неизвестные
координаты вспомогательной функции-вектора
- неизвестные
координаты вспомогательной функции-вектора ![]() . Они
определяются следующим образом
. Они
определяются следующим образом
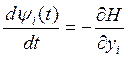 (10)
(10)
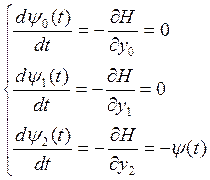 (11)
(11)
![]() находим путем интегрирования:
находим путем интегрирования:
![]() ;
;
![]() ;
;
![]() .
.
Найденные
![]() подставляем в функцию Гамильтона
подставляем в функцию Гамильтона
![]()
Найдем оптимальное управление из решения системы уравнений
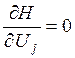 ,
, ![]() (12)
(12)
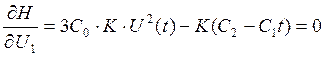
Выразим
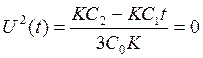
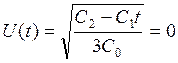 (13)
(13)
Постоянную интегрирования ![]() находят из начальных условий, а К –
заданная величина.
находят из начальных условий, а К –
заданная величина.
Найдем оптимальную траекторию путем интегрирования уравнения (13).
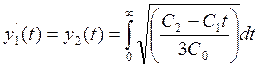
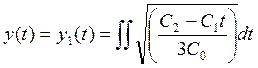
Вывод: в данной лабораторной работе я, используя принцип максимума Понтрягина, нашла оптимальное управление.
Федеральное государственное образовательное учреждение
высшего профессионального образования
“Сибирский Федеральный Университет”.
______________________________________
институт
_____________________________________
кафедра
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2
Решение задач оптимального управления с использованием принципа максимума Понтрягина
Преподаватель _______________ _______________
подпись, дата инициалы, фамилия
Студент_______________ _______________ _______________
код (номер) группы подпись, дата инициалы, фамилия
Красноярск 2010
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.