Решение задач технологического объекта управления с применением

Федеральное государственное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт цветных металлов и материаловедения

Кафедра автоматизации производственных процессов

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

Решение задач ТОУ с применением

принципа максимума Понтрягина

Преподаватель                                                                                  В.А. Осипова

Студент      МФ 07-08                                                                    А.А. Аврамчук

Красноярск 2010

          Цель работы: необходимо за конечное время t_k перевести объект из начального состояние

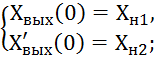
в конечное

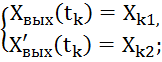
таким образом, чтобы энергия затраченная управляющим устройством была минимальная, то есть

.

          Исходные данные:

Критерий

дифференциальное уравнение

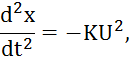
ограничения

          Из данного дифференциального уравнения составим систему линейных дифференциальных уравнений первого порядка.

          Введем обозначения

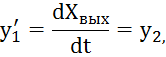
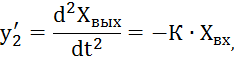
где   Х_вх(t) = U(t).

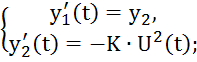
в полученную систему вводим

где

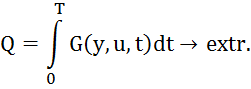
          Дополним полученную систему еще одним уравнением

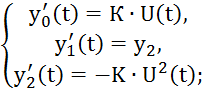
          Составим функцию Гамильтона

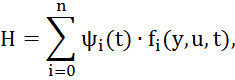
          Находим , ,  которые должны быть непрерывными и ненулевыми

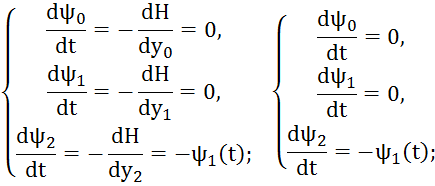
          Найдем  , ,

          Найденные , ,  подставим  в функцию Гамильтона

          Находим оптимальное управление из решения системы уравнений

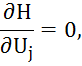
где  j = 1, 2, …, r.

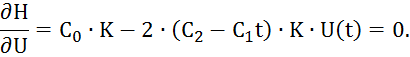
Выразим U(t)

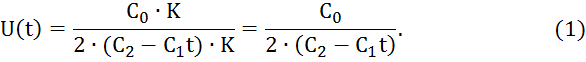
         Найдем оптимальную траекторию путем интегрирования выражения (1)

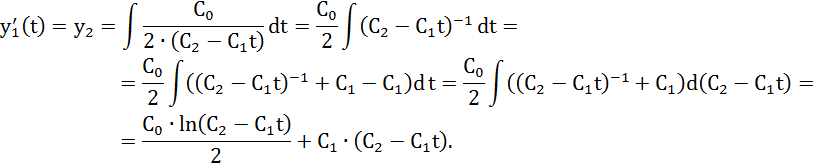
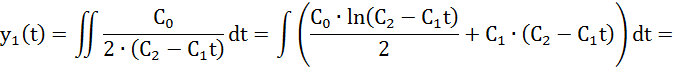
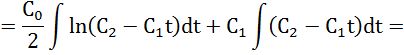
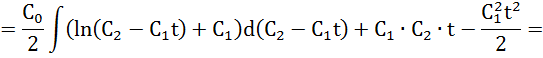
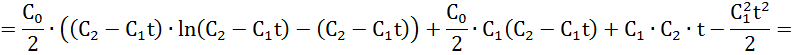
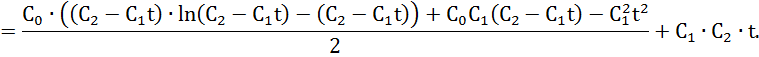
Вывод:  используя принцип максимума Понтрягина, нашел оптимальное управление и оптимальную траекторию.