Расчет автоматической системы регулирования температуры в кубе-испарителе

3 Специальная часть

 В специальной части проекта выполнен расчет автоматической системы регулирования  температуры в кубе-испарителе.

Расчет произведен при максимальном внешнем возмущающем воздействии DX_вх.max = 0,5 мА.

Показатели качества регулирования, определяемые технологическим процессом:

- статическая ошибка, DТ_cт= 0;

- максимальное динамическое отклонение, DТ₁ ≤ 3 °С;

- время регулирования, t_р ≤ 500 с;

- переходной процесс с минимальным квадратичным интегральным показателем (min ∫y² dt).

3.1 Математическое описание объекта управления

Данные кривой разгона приведены в таблице 3.1.

Таблица 3.1 – Исходные данные при А = 0,2 мА ХРО

t, c	0,0	67,5	135,0	180,0	270,0	360,0	405,0	450,0	495,0	540,0
∆T, °C	0,0	0,0	1,0	2,0	4,0	5,5	6,0	6,4	6,7	6,8

Построим график возмущающего воздействия (рисунок 3.1) и кривой разгона объекта (рисунок 3.2).

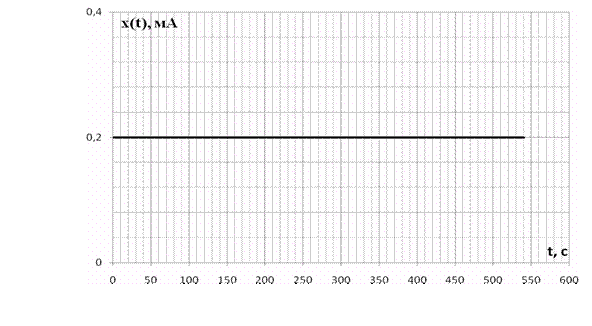
Рисунок 3.1 – График возмущающего воздействия

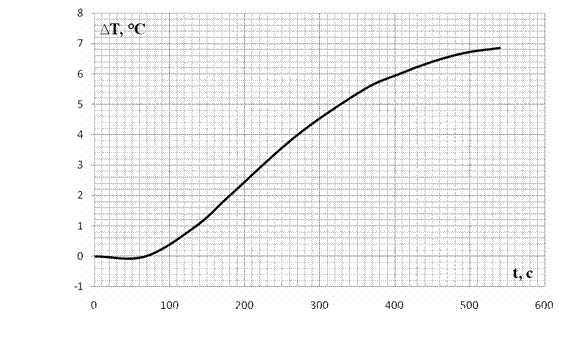
Рисунок 3.2 – График кривой разгона куба-испарителя

Находим единичную ∆T°(t) и нормированную ∆T^н(t) переходные функции

                                              ∆T°(t) = ∆T(t)/А,                                                 (3.1)

                                        ∆T^н(t) = ∆T°(t) /∆T°(T_у),                                          (3.2)

где А – скачкообразное возмущающее воздействие, при котором снята переходная характеристика;

∆T°(T_у) – установившееся значение переходной характеристики.

Результаты расчетов сводим в таблицу 3.2.

Таблица 3.2 – Ординаты переходных функций

t, c	0	67,5	135,00	180,00	270,00	360,00	405,00	450,00	495,00	540,00
DТ(t), °C	0	0,0	1,00	2,00	4,00	5,50	6,00	6,40	6,70	6,80
DТ°(t), °C	0	0,0	5,00	10,00	20,00	27,50	30,00	32,00	33,50	34,25
DТн(t)	0	0,0	0,15	0,29	0,58	0,80	0,88	0,93	0,98	1,00

По данным таблицы 3.2 построены единичная и нормированная переходные характеристики (рисунок 3.3).

Определяем динамические характеристики объекта при аппроксимации его последовательным соединением апериодического звена и звена запаздывания.

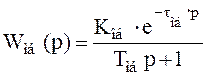                                                           .                                         (3.3)

Находим величину коэффициента усиления объекта К_об

                                                К_об

=∆T°(t_y),                                                   (3.4)

                                              К_об = 34,25 °С/мА.                                              (3.5)

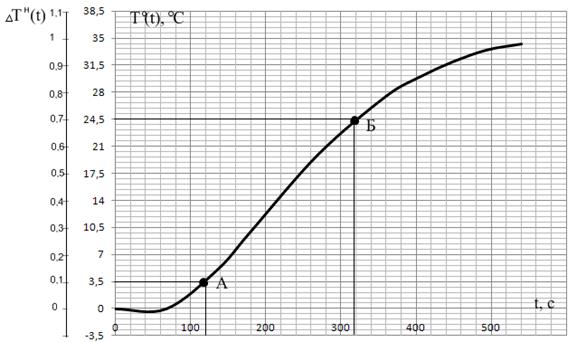
Рисунок 3.3 – Единичная и нормированная переходные характеристики

По нормированной переходной характеристике (рисунок 3.3) определим время t_A и t_Б  для DТ^н(t) = 0,1 и DТ^н(t) = 0,7 соответственно

t_A = 120 – 67,5 = 52,5 с,

t_Б = 315 – 67,5 = 247,5 с.

Теперь определим  дополнительное запаздывание по формуле

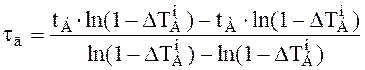                                   ,                                  (3.6)

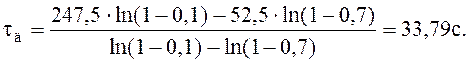
Находим общее запаздывание по формуле

                                                      τ_об = τ+τ_д,                                                  (3.7)

τ_об = 67,5+33,79=101,29 с.

Постоянная времени находится по формуле

                                                 Т_об = 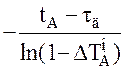,                                               (3.8)

.

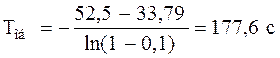Таким образом, подставив значения в формулу 3.3 передаточная функция объекта будет иметь вид

.

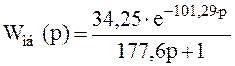Для определения точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения первого порядка с запаздывающим аргументом рассчитываем ординаты аппроксимирующей кривой

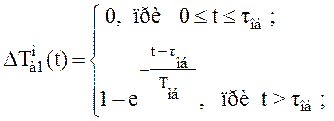                                                             (3.9)

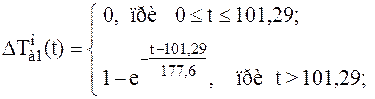
Для нахождения среднеквадратической ошибки аппроксимации вычислим отношение

                                                  d_а1 = {[ΔT^н(t) – ΔТ^н_а1(t)]/ΔT^н(T_y)}².                        (3.10)

Результаты расчетов приведены в таблице 3.3, а аппроксимирующая кривая показана на рисунке 3.5.

Таблица 3.3 – Ординаты переходной функции.

t,c	0	67,5	135,00	180,00	270,00	360,00	405,00	450,00	495,00	540,00
DТн(t)	0	0,0	0,15	0,29	0,58	0,80	0,88	0,93	0,98	1,00
DТнап1(t)	0	0,0	0,17	0,36	0,61	0,77	0,82	0,86	0,89	0,92
da1·10-3	0	0,0	0,07	4,23	0,78	1,37	3,36	5,63	7,71	7,23

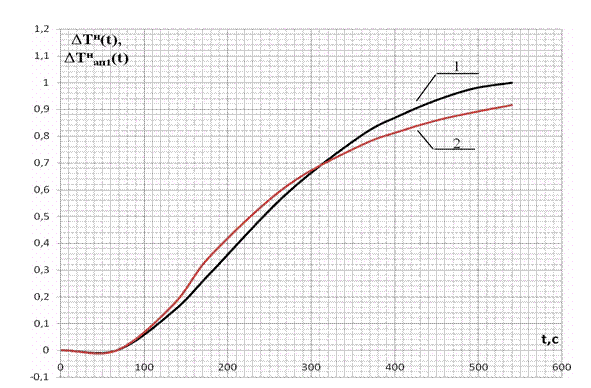
1 – нормированная; 2 – при аппроксимации решением дифференциального

уравнения первого порядка

Рисунок 3.5 – Переходные характеристики объекта

Рассчитаем среднеквадратичную ошибку аппроксимации по формуле

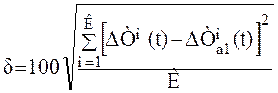                                    ,                                 (3.11)

δ = 5,5%