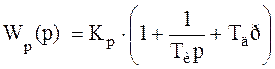Расчет автоматической системы регулирования температуры в кубе-испарителе, страница 3

                                                ,                                   (3.22)

где К_р – коэффициент пропорциональности;  

      Т_и – постоянная времени интегрирования;

      Т_д – постоянная времени дифференцирования

3.3 Определение настроек регулятора для АСР температуры в
 кубе-испарителе

Расчёт настроек регулятора на практике обычно настройки определяют по приближённым формулам, а затем производят их уточнение.

Определим настройки ПИД-регулятора по приближённым формулам [10, таблица 2.2]

                                       К_р = 1,4·Т_об/(К_об·τ_об),                                                (3.23)

                                               Т_и = 1,3·τ_об,                                                      (3.24)

                                               Т_д = 0,5·τ_об.                                                       (3.25)

Подставив значения получаем

К_р = 1,4·177,6/(34,25·101,29) = 0,072 мА,

Т_и = 1,3·101,29 = 131,68 с,

Т_д = 0,5·101,29 = 50,65 с.

Для построения переходного процесса и определения оптимальных настроек регулятора используем ПП VisSim 3.0.

Для оптимизации необходимы начальные значения коэффициентов составляющих ПИД-закона регулирования

                                                             К_п = К_р,                                                    (3.26)

                                                             К_и = К_п/Т_и,                                                 (3.27)

                                                                      К_д = К_п·Т_д                                                             (3.28)

Получаем

К_п = 0,072 мА,

К_и = 0,00055 с,

К_д = 3,65 с.

Переходной процесс с рассчитанными настройками ПИД-регулятора изображен на рисунке 3.7.

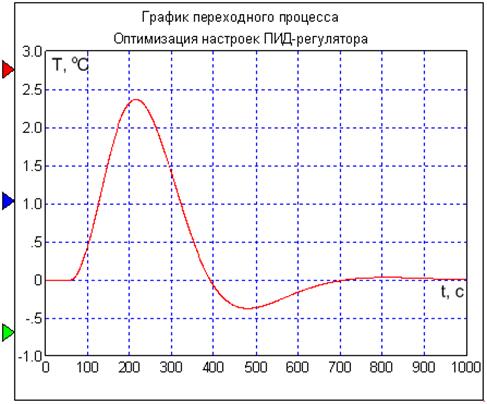
Рисунок 3.7 – Переходной процесс с рассчитанными настройками

ПИД-регулятора

Далее проводим оптимизацию. После проведения оптимизации переходной процесс принимает вид, приведенный на рисунке 3.8.

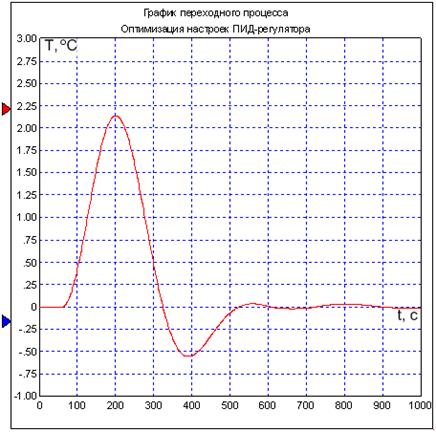
Рисунок 3.8 – Переходной процесс с оптимальными настройками

ПИД-регулятора

В результате проведения оптимизации процесса были получены следующие оптимальные настройки регулятора

К_п = 0,0956;

Т_и = 0,0956/0,00080784 = 118,3 с;

Т_д = 4,95/0,0956 = 51,778 с.

Из графика переходного процесса (рисунок 3.8) видим, что при найденных настройках регулятора время переходного процесса равно 500 с (учитывая коридор равный 0,04 °С) и максимальное динамическое отклонение менее 3 °С, что удовлетворяет заданным показателям качества регулирования процесса.

3.4 Исследование устойчивости системы

Исследуем устойчивость системы регулирования температуры в кубе-испарителе определим запасы устойчивости системы по модулю и по фазе, используя частотный критерий Найквиста.

Для этого рассчитаем АФЧХ объекта и регулятора, которые получают подстановкой p = jωв передаточные функции (3.20) и (3.22).

Передаточная функция объекта примет вид

.

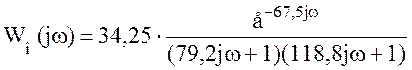Для начала определим АФХ объекта без учета запаздывания

.

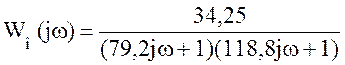Разделим выражение W_о(jω) на вещественную и мнимую части. Для этого умножим числитель и знаменатель W_о(jω) на комплексно-сопряженное знаменателю выражение

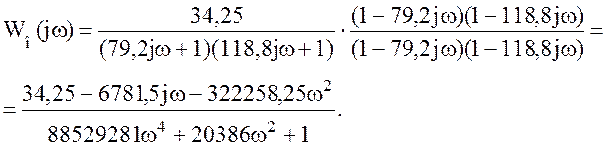
Выражения для вещественной P_o(ω) и мнимой Q_o(ω) частей равны

.

.

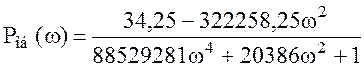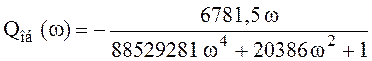 Учтем запаздывание в системе

                                   W_з(jω) = e^-jωτ = cos(ωτ) – jsin(ωτ) = P_з(ω) – jQ(ω).               (3.29)

Тогда АФЧХ объекта будет

W(jω) = W_о(jω)·W_з(jω) = [Р_о(ω) + jQ_о(ω)]·[Р_з(ω) + jQ_з(ω)] = [Р_о(ω)·Р_з(ω) –

 –Q_о(ω)·Q_з(ω)]+j[Q_о(ω)·Р_з(ω) + Р_о(ω)·Q_з(ω)].                    (3.30)

Подставив выражения Р(ω), Q(ω), Р_з(ω),Q_з(ω), получим

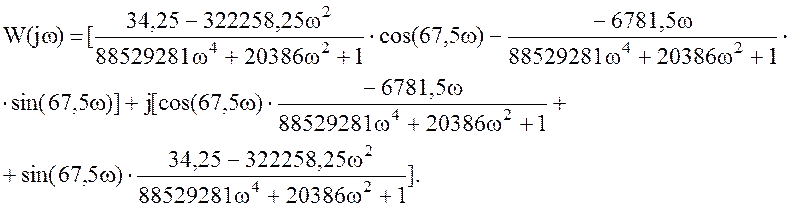
Выразим действительную и мнимую части

,

.

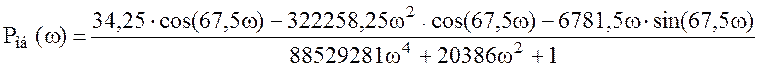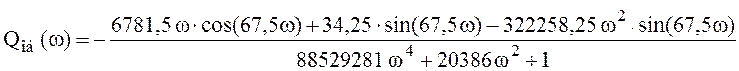  Рассчитаем передаточную функцию регулятора

                                                                                                                                                                                             .

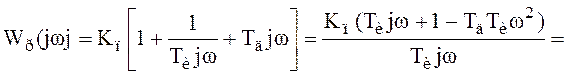
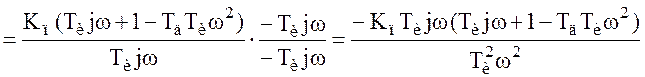Выделим вещественную и мнимую части и подставим значения оптимальных настроек регулятора К_п  = 0,0956,  Т_и = 118,3,  Т_д = 51,778, в результате получим

Р_р(ω) = К_п = 0,0956;