Расчет автоматической системы регулирования температуры в кубе-испарителе, страница 5

По результатам таблицы 3.5 на комплексной плоскости строим АФЧХ системы (рисунок 3.9).

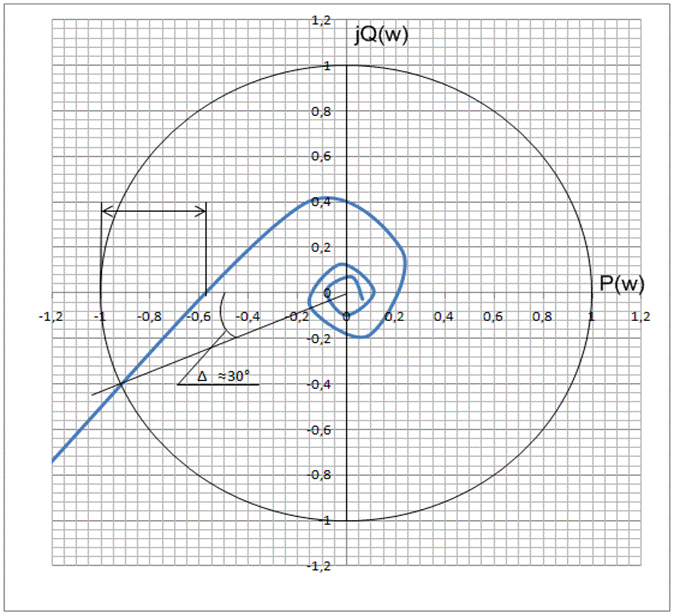
Рисунок 3.9 – АФХ разомкнутой системы

Годограф Найквиста не пересекает точку на комплексной плоскости (–1; j0), поэтому система в замкнутом состоянии является устойчивой и обладает достаточным запасом устойчивости по амплитуде Δa = 0,42 и по фазе Δφ = 30º, что удовлетворяет требуемым показателям качества [11].

 3.5 Проверка настроек регулятора на оптимальность

Для того чтобы убедиться в правильности нахождения настроек регулятора, изменим настройки ПИД-регулятора на 20 % в большую и меньшую сторону (таблица 3.6).

Таблица 3.6 – Настройки регулятора

Переходные процессы, полученные в результате моделирования с начальными настройками регулятора, с оптимальными настройками регулятора, а также с настройками регулятора, увеличенными и уменьшенными на 20 %, представлены на рисунке 3.10.

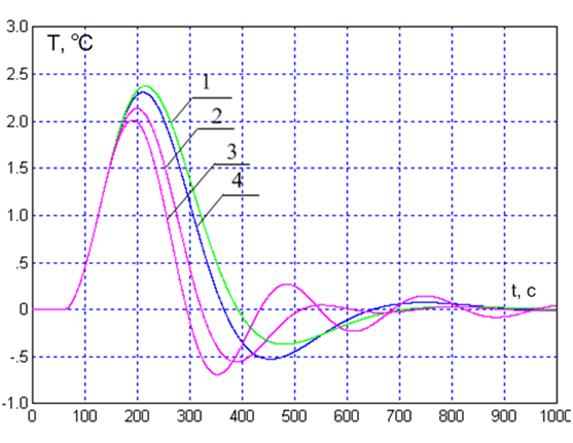
1 – с исходными настройками ПИД-регулятора; 2 – с оптимальными настройками
ПИД-регулятора; 3 – с увеличенными на 20 % настройками ПИД-регулятора; 4 – с уменьшенными на 20 % настройками ПИД-регулятора

Рисунок 3.10 – Переходные процессы в системе

Определим показатели качества полученных процессов, для удобства их восприятия полученные данные сведем в таблицу 3.7.

Таблица 3.7 – Сравнительный анализ показателей качества переходных процессов

Переходной процесс с оптимальными настройками лучше, чем с увеличенными и уменьшенными настройками, так как при изменении настроек
ПИД-регулятора ухудшаются показатели качества, а именно, увеличивается время регулирования и максимального динамического отклонения.

3.6 Построение переходного процесса в АСР при возмущении по заданию

Переходной процесс по заданию представлен на рисунке 3.11

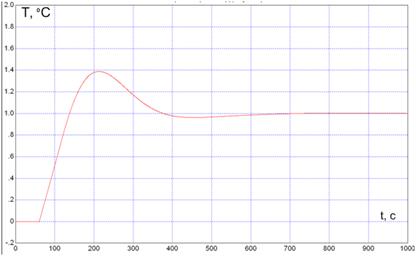
Рисунок 3.11 – Переходный процесс в системе при возмущении по заданию

Определим параметры переходного процесса (рисунок 3.11):

- максимальное динамическое отклонение, ΔТ₁ = 1,4 ºС;

- статическая ошибка, ΔТ_ст = 0;

- время регулирования, t_р = 500 с.

3.7  Проверка системы на грубость

Зачастую параметры объекта управления изменяются во времени. Поэтому

необходимо проверять рассчитанную систему на нечувствительность (грубость) к возможным вариациям параметров системы для наихудших условий. Для проверки нашей системы специально изменим её параметры, а именно, увеличим их на 20 %, и посмотрим, как будет выглядеть переходной процесс в системе. Конечно, нас будут интересовать показатели качества переходного процесса, то есть качество регулирования системы, при изменения параметров объекта, ведь изменять мы будем именно их: К_об и τ_об. На рисунке 3.12 представлен переходной процесс с увеличенными параметрами объекта.

Определяем по графику параметры переходного процесса с увеличенными на 20 % К_об  и τ_об:

- максимальное динамическое отклонение, ΔТ₁ = 2,75;

- статическая ошибка, ΔТ_ст = 0;

- время регулирования, t_р = 3600 с.

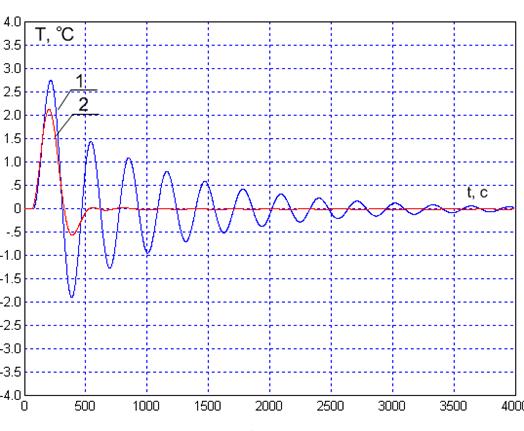
1 – с увеличенными на 20 % параметрами объекта (К_об=41,1, τ_об=81 с);

2 – с исходными параметрами объекта (К_об=34,25 τ_об=67,5 с)

Рисунок 3.12 – Переходные процессы в системе при проверке на робастность

Из рисунка 3.12 видно, что при изменении коэффициента усиления и времени запаздывания качество процесса регулирования сильно ухудшается, но система остается устойчивой, поэтому система является грубой к изменению параметров объекта.