Расчет автоматической системы регулирования температуры в кубе-испарителе, страница 2

Так как ошибка аппроксимации больше допустимого значения 3 %, осуществляем аппроксимацию объекта последовательным соединением двух апериодических звеньев и звена запаздывания (решением дифференциального уравнения второго порядка с запаздывающим аргументом). Передаточная функция будет иметь вид

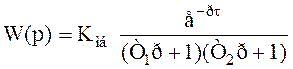                                              ,                                   (3.12)

где Т₁ и Т₂ – постоянные времени объекта.

Находим относительное время по формуле

                                                 ,                                                    (3.13)

.

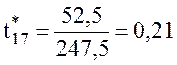По графику [10, рисунок 6.2] найдем значения T^*₁ и T^*₂ и определим действительные значения постоянных времени (T_1, T₂)

Т^*₁ = 0,32,

Т^*₂ = 0,48.

Следовательно

                                                    Т₁ = Т^*₁·t₇,                                                    (3.14)

                                                    Т₂ = Т^*₂·t₇.                                                   (3.15)

Подставив значения получаем

Т₁ = 0,32·247,5 = 79,2,

Т₂ = 0,48·247,5 = 118,8.

 Таким образом, передаточная функция объекта будет иметь вид

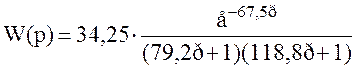                                        .                            (3.16)

Найдем координаты аппроксимирующей кривой по формуле

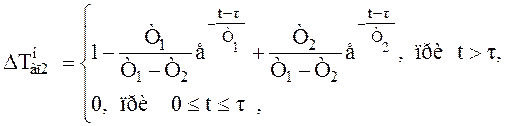                                           (3.17)

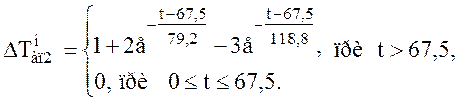
Для нахождения среднеквадратической ошибки аппроксимации вычислим отношение

                                     d_а2 = {[ΔT^н(t) – ΔТ^н_а2(t)]/ΔT^н(T_y)}².                          (3.18)

Результаты расчетов приведены в таблице 3.4, а аппроксимирующая кривая показана на рисунке 3.6.

Таблица 3.4 – Ординаты переходной функции

t,c	0	67,5	135,00	180,00	270,00	36,00	450,00	495,00	540,00
DТн(t)	0	0,0	0,15	0,29	0,58	0,80	0,93	0,98	1,00
DТнап2(t)	0	0,0	0,15	0,32	0,61	0,79	0,89	0,93	0,95
da2·10-3	0	0,0	0,05	0,73	0,63	0,08	1,44	2,60	2,60

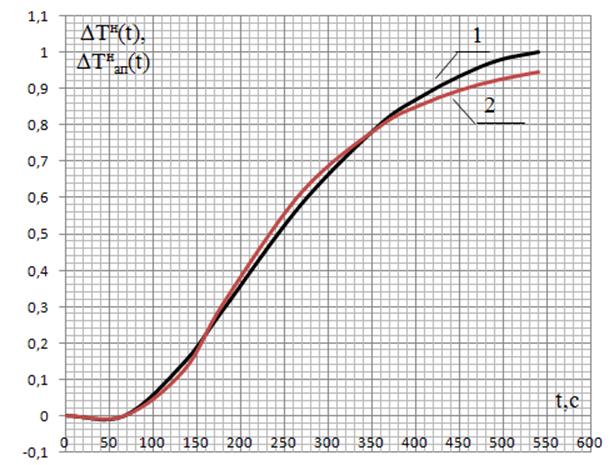
1 – нормированная; 2 – при аппроксимации решением

дифференциального уравнения второго порядка

Рисунок 3.6 – Переходные характеристики объекта

Рассчитаем среднеквадратичную ошибку аппроксимации по формуле

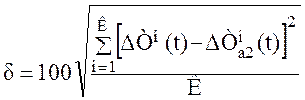                                               .                                (3.19)

δ = 2,94 %.

Так как погрешность аппроксимация меньше 3%, окончательно принимаем передаточную функцию объекта в виде

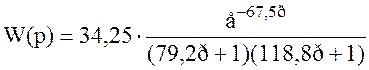                                             .                      (3.20)

3.2 Выбор типа регулятора для АСР температуры в кубе-испарителе

Исходными данными для определения настроек регулятора являются заданные показатели качества регулирования, определяемые технологическим процессом и параметры объекта управления К_об

=34,25, °С/мА, Т_об = 177,6 с, τ_об = 101,29 с.

Тип регулятора выбираем из таблицы [10, таблица 2.1] по отношению

τ_об/Т_об = 101,29/177,6 = 0,57.

В соответствии с этой таблицей  выбираем регулятор непрерывного действия.

Рассчитываем динамический коэффициент регулирования по формуле

                                            R_д = y₁/(К_об·ΔX_вх.max),                                          (3.21)

R_д = 3/34,25·0,5 = 0,175.

По графику [10, рисунок 2.3] определяем, что R_д = 0,175 для требуемого вида переходного процесса, а именно, с минимальным квадратичным интегральным показателем, может обеспечить ПИД-регулятор.

По графику [10, рисунок 2.4] находим для ПИД-регулятора отношение

t_p/τ_об = 10.

Откуда время регулирования

t_р = 10∙τ_об,

t_р = 10·101,29 = 1012,9 с,

что больше допустимого времени регулирования t_р ≤ 500 с.

Несмотря на то, что полученное время регулирования превысило допустимое значение выбираем закон ПИД-регулирования, так как он является наиболее

сложным законом регулирования.

Передаточная функция ПИД-регулятора имеет вид