Промышленность \ Автоматизация технологических процессов и производств

Расчет линейной одноконтурной АСР при возмущении по нагрузке

Страницы работы

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КРАСНОЯРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА

Кафедра АПП

Группа АМЦ – 98 – 2

Дисциплина АТТП

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1

Расчет линейной одноконтурной АСР

при возмущении по нагрузке.

Вариант № 23

Проверил И.И. Лапаев

Выполнил студент М.М. Буженко

Красноярск 2002 г.

Министерство образования Российской Федерации

КРАСНОЯРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ

ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА

Кафедра АПП

Дисциплина АТТП

Группа АМЦ – 98 – 2 Студент Буженко М.М.

ЗАДАНИЕ
ПО РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ № 1

Определить динамическую характеристику отражательной печи для плавки медных концентратов по экспериментальным данным:

Р,Па	8	8	8,07	8,2	8,28	8,5	8,7	8,78	8,84	8,9	8,98	9,08	9,11	9,13	9,15	9,18	9,18
t,сек	0	2	3	4	6	8	10	12	14	16	18	20	22	24	26	28	30

При Х_вх=11% ХРО

Дата выдачи задания “14” февраля 2002г.

Срок сдачи работы “___ ” __________ 200__г.

Руководитель работы ______________ И.И. Лапаев

Расчет линейной одноконтурной АСР при возмущении по нагрузке.

Любой расчет АСР начинается с составления математического описания объекта управления, при котором определяются его статические (коэффициент усиления - К_об) и динамические (запаздывание - t, постоянные времени – Т) параметры.

Расчет ведется при максимальном внешнем возмущающем воздействии, в данном случае DХ_ВХ= 11% ХРО (процентов хода регулирующего органа).

Для расчета АСР используется программный продукт Mathcad.

Найдем отклонение регулируемой величины ∆ Р, Па, данные сведены в таблицу 1.

Определяется единичная D Р⁰(t) и нормированная D Р^Н(t) переходные функции:

D Р⁰(t) = D Р (t) / А,

D Р^Н(t) = D Р⁰(t) / D Р⁰(Т_у),

где А – скачкообразное возмущающее воздействие, при котором снята переходная характеристика (А = 11% ХРО);

∆Р⁰(Т_у) – установившееся значение переходной характеристики.

Результаты сведены в таблицу 1.

Таблица 1 – Ординаты переходных функций

t, сек	0	2	3	4	6	8	10	12
P(t), Па	8	8	8,07	8,2	8,28	8,5	8,7	8,78
∆P(t), Па	0	0	0,07	0,2	0,28	0,5	0,7	0,78
∆P⁰(t), Па	0	0	0,006364	0,018182	0,025455	0,045455	0,063636	0,070909
∆P^н(t), Па	0	0	0,059321	0,16949	0,237285	0,423724	0,593213	0,661009

Продолжение таблицы 1 – Ординаты переходных функций

t, сек	14	16	18	20	22	24	26	28
P(t), Па	8,84	8,9	8,98	9,08	9,11	9,13	9,15	9,18
∆P(t), Па	0,84	0,9	0,98	1,08	1,11	1,13	1,15	1,18
∆P⁰(t), Па	0,076364	0,081818	0,089091	0,098182	0,100909	0,102727	0,104545	0,107273
∆P^н(t), Па	0,711856	0,762703	0,830499	0,915243	0,940667	0,957616	0,974565	0,999988

Окончание таблицы 1 – Ординаты переходных функций

t, сек	30
P(t), Па	9,18
∆P(t), Па	1,18
∆P⁰(t), Па	0,107273
∆P^н(t), Па	0,999988

Графическое отображение таблицы 1 представлено на рисунках: рисунок 1 – график возмущающего воздействия и кривая разгона объекта – давление газа в печи; рисунок 2 – единичная и нормированная переходные характеристики.

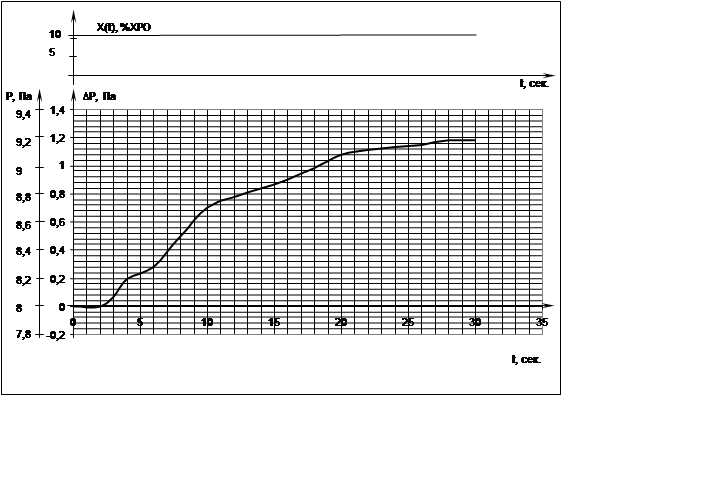Рисунок 1 – График возмущающего воздействия X(t) и кривая разгона объекта Р(t)

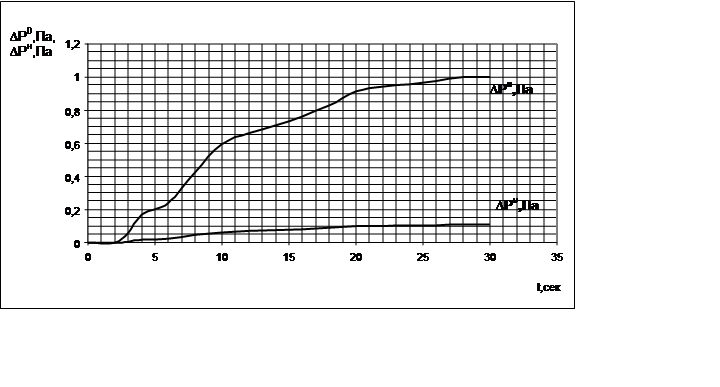
Рисунок 2 - Переходные характеристики: единичная и нормированная

Из зависимости ∆Р^н(t) находим величину коэффициента усиления объекта К_об:

При аппроксимации объекта последовательным соединением апериодического звена и звена запаздывания определяем его динамические характеристики:

I. дополнительное запаздывание

(сек.)

II. общее запаздывание объекта

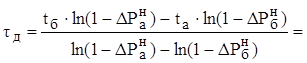
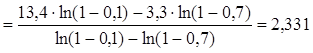(сек.)

III. постоянная времени

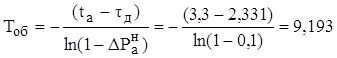(сек.)

Таким образом, передаточная функция объекта имеет вид:

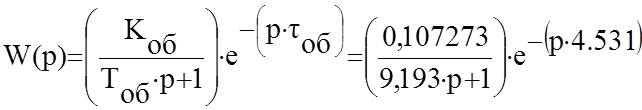
Для определения точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения первого порядка с запаздывающим аргументом рассчитываем ординаты аппроксимирующей кривой:

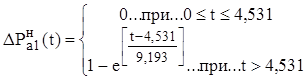
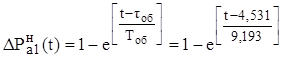
Для нахождения среднеквадратичной аппроксимации вычислим отношение:

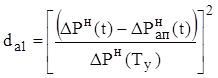
Результаты сводим в таблицу 2.

Таблица 2 – Ординаты переходных функций

t, сек	2	3	4	6	8	10	12
∆P^н(t)Па	0	0,059321	0,16949	0,237285	0,423724	0,593213	0,661009
(t),Па	0	0	0	0,147682	0,314326	0,448387	0,556238
d_а1	0	0,003519	0,028727	0,008029	0,011968	0,020975	0,010977

Продолжение таблицы 2 – Ординаты переходных функций

t, сек	14	16	18	20	22	24	26	28
∆P^н(t)Па	0,71186	0,762703	0,830499	0,915243	0,940667	0,957616	0,974565	0,999988
(t),Па	0,64300	0,712801	0,768954	0,814127	0,850469	0,879705	0,903225	0,922146
d_а1	0,00474	0,00249	0,003788	0,010225	0,008136	0,00607	0,00509	0,00606

Окончание таблицы 2 – Ординаты переходных функций

t, сек	30
∆P^н(t)Па	0,99999
(t),Па	0,93737
d_а1	0,00392

На рисунке 3 показана аппроксимирующая и нормированная переходные характеристики.

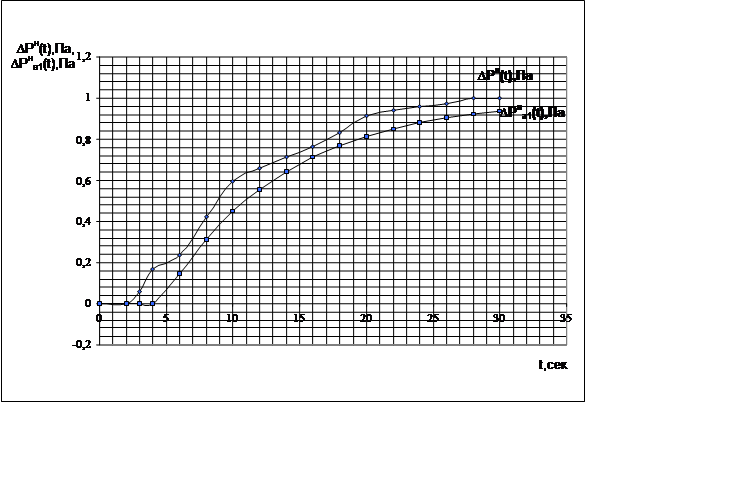
Рисунок 4 – Переходная характеристика при аппроксимации решением дифференциального уравнения первого порядка

Используя данные таблицы 2, рассчитаем среднеквадратичную ошибку аппроксимации:

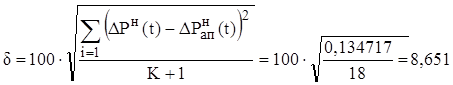
Вывод: В результате проделанной работы были найдены динамические характеристики технологического процесса, а также аппроксимирован объект регулирования с помощью апериодического звена и звена чистого запаздывания. Найденная ошибка аппроксимации является достаточно большой (), следовательно, необходимо осуществлять аппроксимацию объекта последовательным соединением двух апериодических звеньев и звена запаздывания (решением дифференциального уравнения второго порядка с запаздывающим аргументом).