5. Лабораторная работа № 4
ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ И ИНТЕГРИРУЮЩИХ ЦЕПЕЙ
Цель работы
1) Изучить частотные и переходные характеристики простейших цепей и методы их анализа;
2) Изучить возможности использования простейших цепей в качестве интегрирующих и дифференцирующих:
3) Изучить методику расчета основных характеристик интегрирующих и дифференцирующих цепей;
4) Измерить экспериментально основные характеристики интегрирующих и дифференцирующих цепей.
1. Анализ простейших воздействий на элементарные четырёхполюсники
1.1. Воздействие единичного скачка на элементарные четырёхполюсники
В качестве простейших воздействий при анализе электрических цепей используются обычно простейшие сигналы - синусоидальный сигнал, сигнал в виде единичного скачка напряжения или сигнал в виде дельта-импульса. Рассмотрим вначале • воздействия на простейшие цепи сигнала в виде единичного скачка. На рис. 1 показаны элементарные цепи, оставленные из сопротивлений, ёмкостей и индуктивностей. Для анализа цепей используем дифференциальные уравнения. Составим уравнение Кирхгофа для цепи, показанной на рис. 1, а. Для неё уравнение Кирхгофа имеет вид:
![]() (1.1)
(1.1)
Известно для ёмкости, что 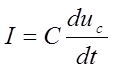
![]() тогда
тогда 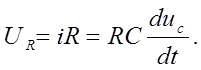 , В ре зультате получаем уравнение
, В ре зультате получаем уравнение
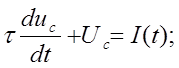
![]() (1.2)
(1.2)
Аналогично для цепи, показанной на рис. 1, г имеем уравнение Кирхгофа
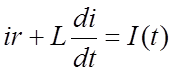
или
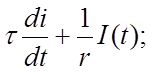
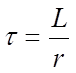 (1.3а)
(1.3а)
Объединяя оба приведенных уравнения в общем, виде получаем
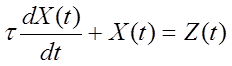 (1.3б)
(1.3б)
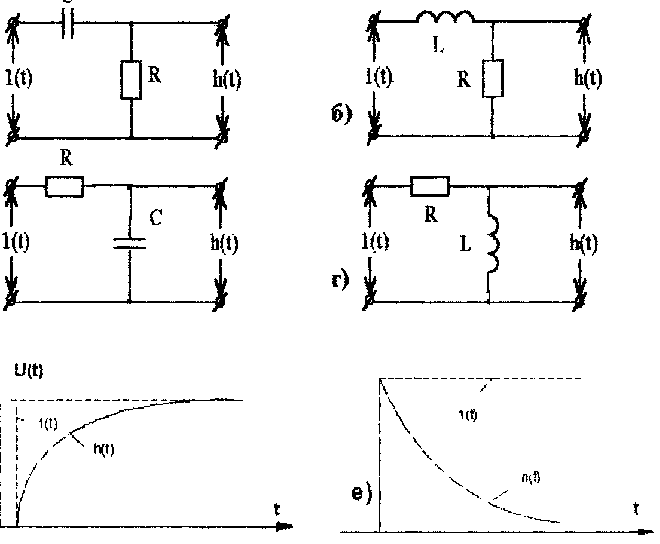
Рис. 1 Схемы и переходные характеристики простейших четырёхполюсников
Из математики известно, что для таких уравнений общее решение можно представить в виде
![]()
где ![]() -
частное решение уравнения (1.3);
-
частное решение уравнения (1.3); ![]() - общее решение однородного уравнения вида
- общее решение однородного уравнения вида
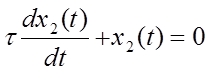
Известно также, что ![]() следует искать в виде
следует искать в виде 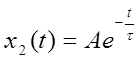 и тогда получаем
и тогда получаем
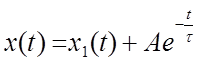 (1.4)
(1.4)
Очевидно, что в полученном решении величину x(t) можно рас сматривать как сумму двух величин:
![]() - слагаемое,
представляющее собой значение x(t)в установившемся режиме и
- слагаемое,
представляющее собой значение x(t)в установившемся режиме и 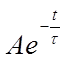 - слагаемое,
характеризующее переходной процесс в схеме.
- слагаемое,
характеризующее переходной процесс в схеме.
Действительно, при 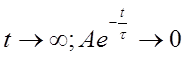 поэтому
поэтому ![]() , тогда
, тогда
При t = 0 находим ![]() , откуда
, откуда ![]()
Таким общее решение уравнения (1.3) будет
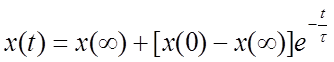
Применим полученное решение для анализа
цепей, показанных на рис. 1 при единичном воздействии, Напряжение на выходе
четырёхполюсника в этом случае называют переходной характеристикой и
обозначают ![]() т.е. в нашем случае
т.е. в нашем случае ![]() . Например, для цепей, показанных на рис 1,а
и б из физических соображений (из свойств ёмкости и индуктивности)
следует, что
. Например, для цепей, показанных на рис 1,а
и б из физических соображений (из свойств ёмкости и индуктивности)
следует, что ![]()
![]() и,
следовательно,
и,
следовательно,
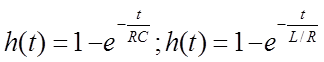 (1.6)
(1.6)
Для цепей, показанных на рис.1 в и г
из физических соображений следует, что ![]()
![]() ,
т.е.
,
т.е.
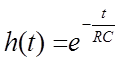 и
и 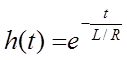 (1.7)
(1.7)
Графики напряжении, построенные по формулам (1.6, 1.7) показаны соответственно на рис. 1, д и е.
1.2. Воздействие синусоидального сигнала на элементарные четырёхполюсннники
Пусть на входе схемы рис, 1, а действует синусоидальное напряжение
![]() (1.8)
(1.8)
Для расчета реакции цепи воспользуемся методом комплексных амплитуд, Комплексная амплитуда тока в цепи равна
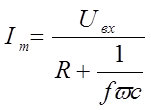 (1.9)
(1.9)
Следовательно ,выходное напряжение схемы будет равно
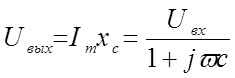 ,
, ![]() (1.10)
(1.10)
Коэффициент передачи схемы по напряжению равен
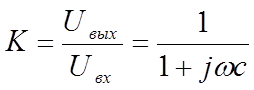 (1.11а)
(1.11а)
Амплитудно-частотная и фазо-частотная характеристики цепи определяются выражениями:
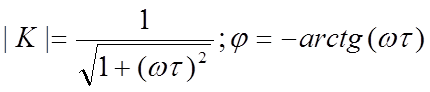 (1.11б)
(1.11б)
Аналогичным образом для цепи, показанной на рис. 1, в нетрудно нполучить выражения для амплитудно-частотной и фазо-частотной характеристик цепи. Эти выражения имеют вид
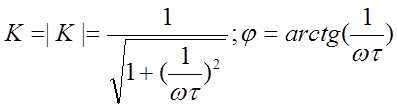 (1.12)
(1.12)
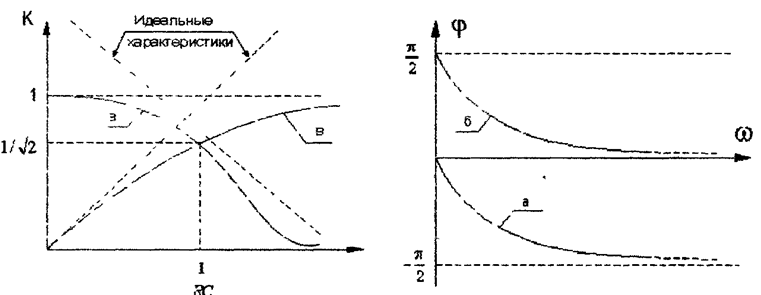
С помощью формул (1.11, 1.12) построены амплитудно-частотные и фазовые характеристики цепей, показанные на рис.2.
а) б)
Рис.2 Частотные характеристики четырёхполюсников
Рассмотрение частотных характеристик
простейших четырёхполюсников (на рис. 2 с индексом «а» показаны кривые,
относящиеся к рис, 1, а и с индексом «в» - к рис. 1, в) показывает,
что схема рис. 1, а обеспечивает почти без ослабления передачу сигналов
с низкими частотами 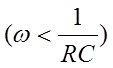 , поэтому схемы рис. 1, а и
б иногда называют схемами фильтров низких частот. Зависимость фазового
сдвига от частоты в области низких частот почти линейная, что соответствует
неискажённой передаче сигналов.
, поэтому схемы рис. 1, а и
б иногда называют схемами фильтров низких частот. Зависимость фазового
сдвига от частоты в области низких частот почти линейная, что соответствует
неискажённой передаче сигналов.
Для цепей, показанных на рис. 1, в и
г, неискажённая передача сигналов почти без ослабления
обеспечивается в области частот 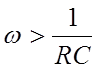 , поэтому эти
схемы иногда называют фильтрами верхних частот. Цепь, показанную на рис. 1, в
часто используют в усилительных каскадах в качестве разделительной,
переходной цепи. В этом случае постоянную времени цепи выбирают достаточно
большой, что обеспечивает ослабление сигналов только на частотах близких к
нулю, в основном же все усиливаемые сигналы передаются без искажения и
ослабления, В то же время такая цепь обеспечивает разделение каскадов по
постоянному напряжению.
, поэтому эти
схемы иногда называют фильтрами верхних частот. Цепь, показанную на рис. 1, в
часто используют в усилительных каскадах в качестве разделительной,
переходной цепи. В этом случае постоянную времени цепи выбирают достаточно
большой, что обеспечивает ослабление сигналов только на частотах близких к
нулю, в основном же все усиливаемые сигналы передаются без искажения и
ослабления, В то же время такая цепь обеспечивает разделение каскадов по
постоянному напряжению.
1.3. Элементарные четырёхполюсники при воздействиях произвольного вида
Вкратце рассмотрим как осуществляется анализ реакции простейших четырёхполюсников при воздействиях произвольного вида.
При воздействии периодических сигналов произвольной формы на простейшие четырёхполюсники осуществляется с помощью операционного метода. В этом случае, например для цепи, показанной на рис. 1, а, коэффициент передачи четырёхполюсника записывается в операционной форме (из формулы 1.11а)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.