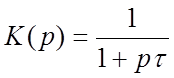Исследование дифференцирующих и интегрирующих цепей, страница 2

                                       (1.13)

Входное воздействие 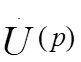  также представляется в операционной форме. Выходное воздействие в этом случае определяется соотношением 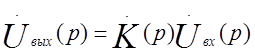    , что дает для случая единичного скачка, имеющего изображение ,  дает

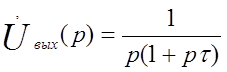.                                  (1.14)

Воспользовавшись таблицей соответствия изображений и оригиналов

можно найти, что

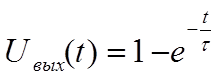                                    (1.15)

Последнее равенство естественно  совпадает  с  формулой  (1.6).  Для прямоугольного импульса, на входе имеющего изображение

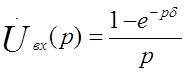,                                                        (1.16)

на выходе получим

,

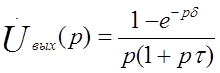вводя обозначение 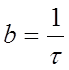  приводим к табличному виду:

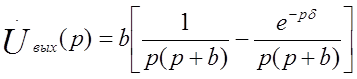                       (1.17)

Здесь δ-длительность импульса.

Из таблиц соответствия оригиналов и изображении можно найти, что

при t < δ    

при  t > δ   

Форма передаваемою импульса при различных значениях параметров

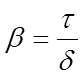   показана на рисунке 3, а.

Аналогичным образом для перехода цепи (рис.1,в) получают

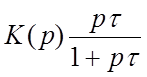    и при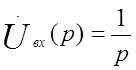  

(1.19)

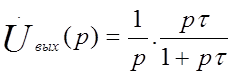
Последнему выражению соответствует  оригинал в форме (1.7). Форма выходного сигнала при воздействии на вход цепи прямоугольного  импульса показана на рисунке   3, а. На участке действия импульса длительностью происходит заряд конденсатора, и напряжение на выходе это время убывает по экспоненциальному закону.

После окончания действия импульса конденсатор начинает разрежается через сопротивление и источник входного сигнала. Начало заряда сопровождается скачком выходного напряжения в отрицательном направлении, Время заряда и разряда конденсатора определяется постоянной времени цепи. От постоянной времени цепи τ зависит и длительность выходного импульса.

Определённые особенности имеет анализ реакции рассматриваемых четырёхполюсников на воздействие случайных сигналов. В этом случае используют понятия энергетического спектра, корреляционной функции и коэффициента передачи мощности. Возможности применения этих понятии  к простейшим четырёхполюсникам   покажем  на примере схемы рис . 1, а.

Энергетический спектр выходного сигнала  связан с энергетическим   спектром входного сигнала соотношением

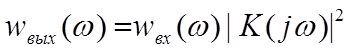,                       (1.20)

      -коэффициент  передачи четырехполюсника по  мощности.

Корреляционная функция выходного сигнала имеет вид

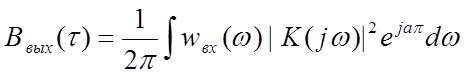              (1.21)

где τ- интервал корреляционной функции,

Мощность шума на выходе четырёхполюсника

Если на входе четырёхполюсника рис. 1, а действует источник белого шума с постоянным на всех частотах энергетическим спектром W₀, то указанные выражения примут следующие конкретные значения.

Коэффициент передачи цепи по мощности

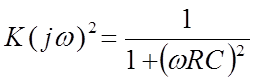                             (1.22)

Автокорреляционная функция выходного сигнала

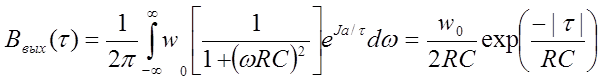  (1.23)

Энергетический спектр выходного сигнала

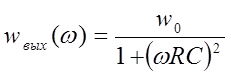                                  (1.24)

Мощность выходного сигнала

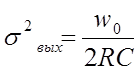                                       (1.25)

Графики корреляционной функции и спектра показаны на рис. 4.

а)                                                                               б)

Рис. 4 Характеристики случайного процесса на выходе простейшего четырёхполюсника

2. Дифференцирующие и интегрирующие цепи

2.1 Идеальные интегрирующие и дифференцирующие цепи

Вначале дадим определения, что понимается под идеальной интегрирующей и дифференцирующей цепью.

Дифференцирующей цепью называется линейный четырёхполюсник, у которого выходное напряжение пропорционально производной от входного напряжения_, т.е.

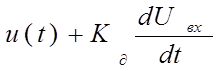                                              (2.1)

Интегрирующей цепью называется линейный четырёхполюсник, напряжение на выходе которого пропорционально интегралу от входного напряжение, т.е.

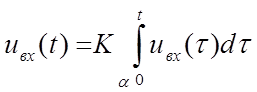                                       (2.2)

В формулах (2.1; 2.2) ,-коэффициенты пропорциональности.

Допустим на входе дифференцирующей и интегрирующей цепей действует синусоидальный сигнал. В этом случае для дифференцирующей цепи получаем

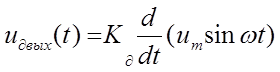
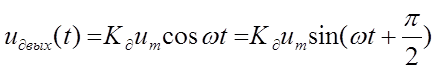                   (2.3)

и для интегрирующей цепи находим

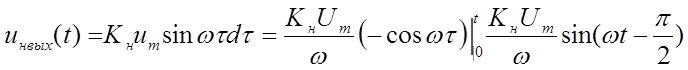  (2.4)

(без учёта постоянной интегрирования).

Таким образом, получено для дифференцирующей цепи, что модуль коэффициента передачи равен

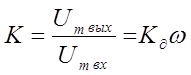                                        (2.5а)

и фазовый сдвиг равен .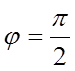

Соответственно для интегрирующей цепи получим