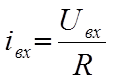Исследование дифференцирующих и интегрирующих цепей, страница 4

 (зажимы (+) и (—) соединены накоротко).

Этот ток заряжает конденсатор С и создаёт на нём напряжение, которого является выходным. Связь между током и напряжением на конденсаторе как известно определяется соотношением

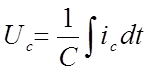                                                (2.11)

или учитывая значение получаем

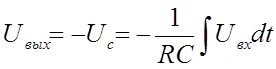                          (2.12)

Таким образом схема с идеальным ОУ является идеальным интегратором. Естественно, что схемы реальных ОУ дают результаты отличающиеся от реальных.

В дифференцирующем каскаде (рис. 5,б) в силу принципа виртуального замыкания (вход (—) заземлён) напряжение на входе является напряжением на конденсаторе. Заряжающий конденсатор ток 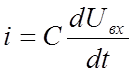. Этот ток не заходя в усилитель, полностью проходит через сопротивление R, создавая на нём напряжение, являющееся выходным:

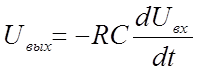                                (2.13)

Таким образом схема с идеальным операционным усилителем является идеальным дифференциатором. Реальные схемы ОУ обеспечивают дифференцирование с определённой погрешностью.

3. Расчётная часть

3.1 Основные расчётные соотношения и исходные данные

а) Расчёт переходных характеристик

Расчёт переходной характеристики интегрирующей цепи выполняется по формуле:

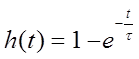                                                 (3.1)

 а для дифференцирующей цепи по формуле:

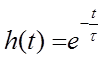                                                       (3.2)

где τ - постоянная времени цепи равная τ = RC

б) Расчёт частотных характеристик

Расчёт  амплитудно-частотной и фазо-частотной характеристик интегрирующей цепи осуществляется по формулам:

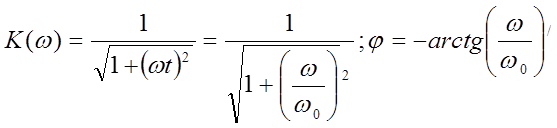       (3.3)

а для дифференцирующей цепи по формулам:

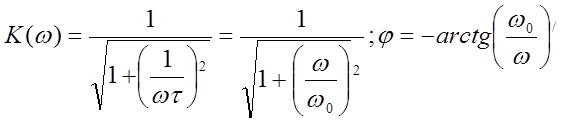         (3.4)

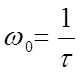  частота среза  фильтра.

Исходные данные для расчёта в соответствии с номиналами элементов, входящих в комплект "Луч" представлены в таблице.

Расчёт частотных характеристик осуществляется в соответствии с формулами (3.3; 3.4). Расчеты свести в таблицы. Форма таблицы показана ниже.

Таблицы расчёта характеристик простейших цепей

Таблица расчёта переходных характеристик

Таблица 3.2.1

Таблица расчёта частотных характеристик

Таблица 3.2.2

4. Экспериментальное исследование дифференцирующих и интегрирующих цепей

4.1 Снятие переходных характеристик цепей