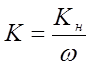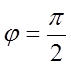Исследование дифференцирующих и интегрирующих цепей, страница 3

;                                            (2.6а)

Сравним полученные выражения для коэффициентов передачи идеальных интегрирующих и дифференцирующих цепей для следующих условий

или 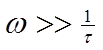    (2.7)   и  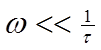   (2.8)

с коэффициентами передачи цепей, показанных на рис. 1, а и в и определяемых формулами (1.11) и (1.12).

При условии (2.7) из формулы (1.11) находим

10

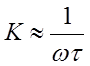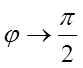, или обозначив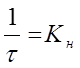 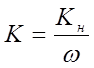                        (2.5б)

аналогично для  условий (2.8) находим,

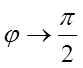;     или обозначив   ;                            (2.5б)

И так получено, что при определённых условиях цепи, показанные на рис, 1, а и б могут играть роль интегрирующих цепей, а цепи, показанные на рис, 1, в и г могут играть роль дифференцирующих цепей. Сравнение реальных частотных характеристик указанных цепей с частотными характеристиками идеальных интегрирующих и дифференцирующих цепей, показанными на рис. 2, а пунктиром показывает, что совпадение этих характеристик достаточно хорошее в области низких частот для дифференцирующей цепи и в области высоких частот для интегрирующей цепи.

2.2 Схемная реализация интегрирующих и дифференцирующих цепей

Дифференцирующие и интегрирующие цепи в реальных часто реализуются в виде простейших четырёхполюсников, воображённых на рис. 1, в и 1, а соответственно. Из рис. 3, а видно, что при прохождении прямоугольного импульса через реальную цепь вместо линейного нарастания и спада напряжения,, имеющего место при идеальном интегрировании, изменения напряжения происходят по экспоненциальному закону.

в)                                                                  б)

Рис. 3 Прохождение прямоугольного импульса через простейшие четырёхполюсники

 На выходе дифференцирующей цепи вместо дельта-импульса, имеющего при идеальном дифференцировании единичного скачка на выходе реальной цепи приучаются также два экспоненциальных импульса. Эти отклонения обусловлены различиями реальных и идеальных интегрирующим и дифференцирующих цепей.

Условия (2.7) и (2.8) показывают какими должны быть требования, предъявляемые к интегрирующим и дифференцирующих  цепям. Практически же известно, что чем сильнее выполняются приведённые неравенства, тем меньше коэффициент передачи дифференцирующей и интегрирующей цепей. Поэтому параметры этих цепей выбирают исхода из компромисса между требованиями ж точности дифференцирования (интегрирования) и требованиями к коэффициенту передачи.

С учётом этих требований постоянные времени выбирают для интегрирующей цепи

τ = RC =5 τ_u                                                                  (2.9)

и для дифференцирующие цепи

τ = RC = 0,1τ_ф                                                   (2.10)

где τ_u,τ_ф -соответственно длительность импульса и его фронт

Рассмотрение дифференцирующих и интегрирующих цепей на
основе сопротивлений и ёмкостей показывает, что с помощью таких
цепей принципиально невозможно осуществить идеальное дифференцирование и интегрирование. Поиск более рациональных схемных решений привёл к использованию дифференцирующих и интегрирующих цепей на базе операционных усилителей. Схемы интегрирующего и дифференцирующего каскада с использованием ОУ показаны на рис. 5, а и  б соответственно.

а)                                                           б)

Рис. 5 Схемы интегрирующего и дифференцирующего каскадов

При анализе схем на основе операционных усилителей обычно делаются допущения, позволяющие значительно упростить анализ схем. ОУ считается в идеальным. Идеальным называют такой ОУ, у которого входное сопротивление для разностного сигнала и коэффициент усиления для этого сигнала равны бесконечности, а выходное сопротивление равно нулю. Кроме того предполагается,, что коэффициент ослабления синфазного сигнала равен бесконечности. Большое значение коэффициента усиления позволяет считать, что напряжение между зажимами (+) и (—) ОУ равно нулю. Вследствие большого входного сопротивления считают равным нулю. Вследствие большого входного сопротивления считают равным нулю и ток, ответвляющийся на вход усилителя. Такое состояние зажимов (+) и (—) усилителя соответствует принципу виртуального замыкания. При виртуальном замыкании, как и при обычном, напряжение между замкнутыми зажимами равно нулю. Однако, в отличие от обычного замыкания, ток между виртуально замкнутыми зажимами не течёт, т.е. в виртуальное замыкание ток не ответвляется. Иначе говоря, для тока виртуальное замыкание эквивалентно разрыву цепи. Используя принцип виртуального замыкания применительно к схеме рис. 5, а можно считать, что ток через резистор R равен