атомов примеси [см-2-с-1]; N — концентрация атомов примеси [см-3]; D — коэффициент диффузии [см2-с-1]. Знак минус указывает на то, что движение вещества происходит в направлении уменьшения его концентрации.
|
|
Коэффициент диффузии Dчисленно равен количеству примесных атомов, проходящих через площадку 1 см2 за 1 с при градиенте концентрации атомов примеси, равном 1 см -4. Иначе говоря, коэффициент диффузии представляет собой плотность потока при единичном градиенте концентрации.
Изменение коэффициента диффузии с температурой описывается уравнением Аррениуса:
![]() (2)
(2)
где k = 8,63-10 -5 эВ/К — постоянная Больцмана; Т—абсолютная температура процесса [К]; Еа — энергия активации процесса диффузии [эВ], равная 3,7 эВ для В и 4,4 эВ для Р; Д0— коэффициент [см2 с -1], зависящий от рода полупроводника и диффундирующей примеси, от кристаллографического направления и от концентрации исходной примеси. При диффузии в беспримесный кремний с ориентацией поверхности кристалла {111} D0= 14 (для бора) и 1500 см2-с -1 (для фосфора).
 Расчет коэффициента
диффузии по уравнению Аррениуса затруднен, так как энергия
активации Еа зависит как от рода полупроводника и диффундирующей
примеси, так и от концентрации вводимой
N0 и
исходной Nисх примесей
легируемой заготовки. При температуре диффузии вводимая и исходная примеси оказываются частично или полностью
ионизированными, в результате чего
возникает ускоряющее электрическое
поле, уменьшающее энергию активации и повышающее коэффициент диффузии.
Расчет коэффициента
диффузии по уравнению Аррениуса затруднен, так как энергия
активации Еа зависит как от рода полупроводника и диффундирующей
примеси, так и от концентрации вводимой
N0 и
исходной Nисх примесей
легируемой заготовки. При температуре диффузии вводимая и исходная примеси оказываются частично или полностью
ионизированными, в результате чего
возникает ускоряющее электрическое
поле, уменьшающее энергию активации и повышающее коэффициент диффузии.
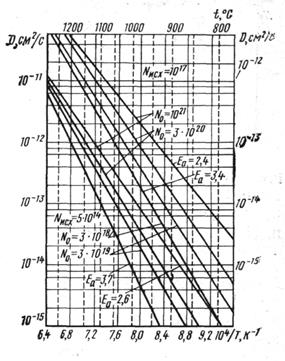
 На рис. 2 представлены температурная и концентрационная зависимости
коэффициента диффузии фосфора в кремний.
Здесь же приведены действительные значения
энергии активации, которые характеризуют тангенс угла наклона прямых
на графике в соответствии с уравнением
На рис. 2 представлены температурная и концентрационная зависимости
коэффициента диффузии фосфора в кремний.
Здесь же приведены действительные значения
энергии активации, которые характеризуют тангенс угла наклона прямых
на графике в соответствии с уравнением
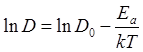 (3)
(3)
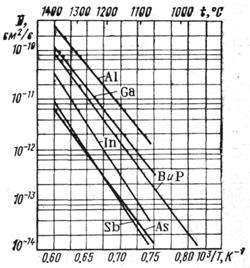
 На
рис.3 приведена температурная зависимость коэффициента диффузии для различных
легирующих элементов в кремнии,
легированном с NИСХ=5 10-14
см -3 при концентрации диффундирующей примеси N0=3 1019 см -3. На
практике в качестве легирующих примесей для кремниевых структур обычно используют бор (акцептор) и фосфор (донор).
На
рис.3 приведена температурная зависимость коэффициента диффузии для различных
легирующих элементов в кремнии,
легированном с NИСХ=5 10-14
см -3 при концентрации диффундирующей примеси N0=3 1019 см -3. На
практике в качестве легирующих примесей для кремниевых структур обычно используют бор (акцептор) и фосфор (донор).
Диффузионный профиль. Чтобы рассчитать режимы процесса диффузии, необходимо знать закон распределения примеси по глубине диффузионной области.
![]()
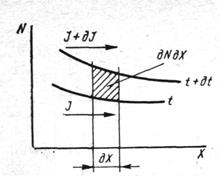 Рассмотрим
площадку 1 см2 толщиной дх(рис. 4).Очевидно,
чтоизменение
числа атомов примеси в элементарном объеме за время дtдолжно быть равно изменению
плотности потока на интервале дх за то же время, т. е. дNдx= -дJдt.
Рассмотрим
площадку 1 см2 толщиной дх(рис. 4).Очевидно,
чтоизменение
числа атомов примеси в элементарном объеме за время дtдолжно быть равно изменению
плотности потока на интервале дх за то же время, т. е. дNдx= -дJдt.
Знак минус указывает на то, что накопление примеси имеет место только при уменьшении плотности потока в направлении оси х. Используя выражение (1), получим второе уравнение (закон) Фика:
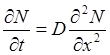 (4)
(4)
Этот закон определяет скорость накопления примеси, т. е. отражает динамику процесса. В уравнениях (1) и (4) коэффициент Dпринимают постоянным во времени и по глубине х.
Закон распределения примеси как функция координаты х и времени может быть получен путем решения второго уравнения Фика при определенных граничных условиях, т. е. при определенных условиях проведения процесса. Наибольшее практическое значение имеют два случая.
В случае неограниченного (постоянного) источника примеси
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.