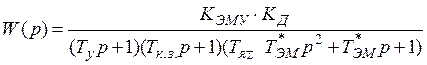Анализ и синтез линейных автоматических систем регулирования, страница 3

, (1.16)

где T_Я_S = 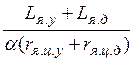– суммарная постоянная времени цепи якоря ЭМУ и двигателя, с;

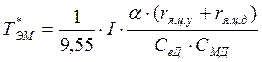– электромеханическая постоянная времени двигателя при работе от ЭМУ, с.

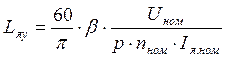, (1.17)

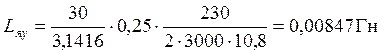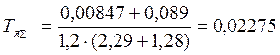с,

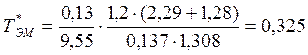Передаточная функция ЭМУ с двигателем:

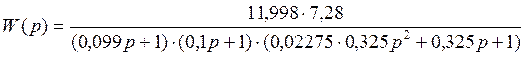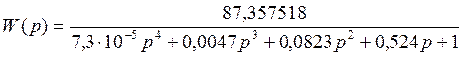1.2.3 Передаточная функция тахогенератора и ее расчет

Передаточная функция тахогенератора имеет вид:

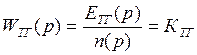. (1.18)

Для расчета воспользуемся данными приведенными в таблице 3 и получим:

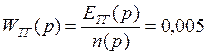1.3 Нахождение передаточной функции АСР

Передаточная функция АСР:

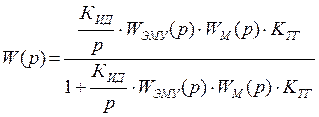, (1.19)

1.4 Исследование устойчивости АСР

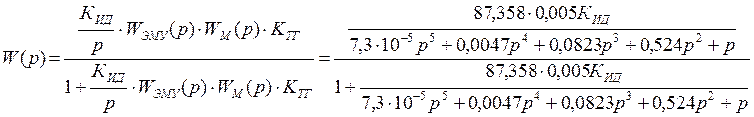
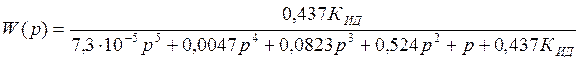Устойчивость АСР определяем по критерию Гурвица. Определитель Гурвица для системы пятого порядка будет иметь вид:

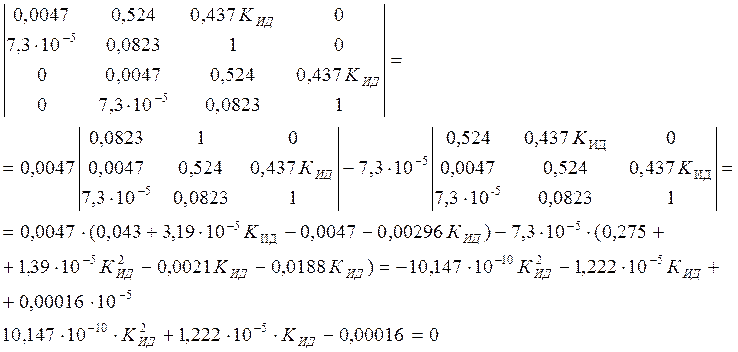
Находим дискриминант

Вычисляем К_ИД.

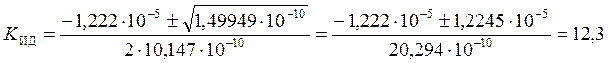
Выбираем К_ИД, с условием, что

Необходимо обеспечить 60% запас устойчивости, поэтому: , главный определитель Гурвица будет больше нуля.

Тогда передаточная функция системы будет иметь вид:

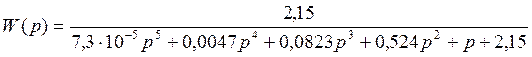Для построения ВЧХ подставляем в передаточную функцию замкнутой системы p = jw:

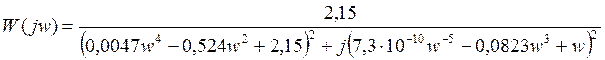
Домножим на сопряженные и выделим вещественную часть:

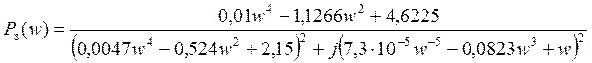
Изменяя значения w от 0 до ¥ находим значения . Полученные данные сведены в таблицу 4.

Таблица 4 – Значения ВЧХ

P(w)	1	1,001	0,860	0,539	0,151	-0,853	-0,870	-0,405	-0,192	-0,023	0,002	0
w	0	1	1,5	1,8	2	2,5	3	4	5	8	11

По данным таблицы 4 строим вещественную частотную характеристику рисунке 3.

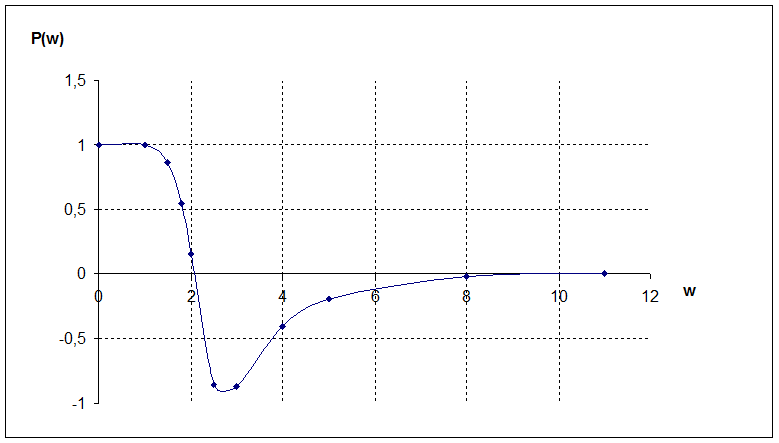
Рисунок 3 – Вещественная частотная АСР

1.5 Построение переходного процесса методом трапеций.

1.5.1 Разбивка ВЧХ на трапеции.

Разбиваем ВЧХ на трапеции по правилам разбивки (рисунок 4).

Для каждой трапеции определим высоту r, частоты и , величину

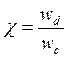. (1.20)

Данные сведем в таблицу 5.

Таблица 5 – Параметры трапеций

Рисунок 4 – Разбиение ВЧХ на трапеции

Проверка: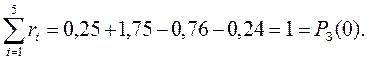

Составим для каждой трапеции таблицу h(t)-функций, в которой укажем значения и t , а также значения функций h() и h(t). Расчет ведется по формулам:

, (1.20)

. (1.21)

Таблица 6 – Значения h(t)-функций для трапеций 4 и 3 соответственно

1 2 3 4 5 6