Теоретический закон распределения. Доверительный интервал, страница 8

D = ∑[y_i – f(x_i, C₁, C₂, …, C_k)]² = F(C₁, C₂, …, C_k) = min

Для максимально точной аппроксимации надо:

      ∂D / ∂C₁ = 0; ∂D / ∂C₂ = 0; …; ∂D / ∂C_k = 0

или:

                         ∑[y_i – f(x_i, C₁, C₂, …, C_k)] * ∂F / ∂C₁ = 0

…

∑[y_i – f(x_i, C₁, C₂, …, C_k)] * ∂F / ∂C_k = 0

В нашем случае:

                        ∑[t_i – c1*sin(c2*x_i)] * sin(c2*x_i) = 0

                        ∑[t_i – c1*sin(c2*x_i)] * c1*c2*cos(c2*x_i) = 0

                   Преобразуем систему к виду:

                      ∑t_i* sin(c2*x_i) – ∑c1*sin²(c2*x_i) = 0

                      ∑t_i*c1*c2*cos(c2*x_i) – ∑c1²*c2*sin(c2*x_i)*cos(c2*x) = 0

Решив эту систему найдём: c1=7.0026, c2=0.2664                       

Найдем значения данной функции в точках x_i  составим таблицу 4.4.

Таблица 4.4

Xi, мм	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
ti, мc	0,0	1,84	3,56	5,02	6,13	6,8	7,0	6,7	5,93	4,4

Нарисуем график по таблице 4.4

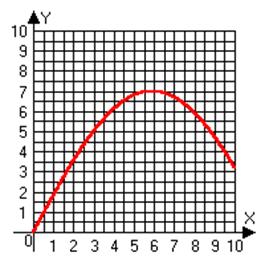
Определим точность нахождения аппроксимирующей функции: 

методом наименьших квадратов и составим таблицу 4.5

Таблица 4.5

№ измерения	ti,мc.	t0i,мc.	Δt,мc.	ε,%
1	0	0	0,0	0
2	2,4	1,84	0,56	23,3
3	4,2	3,56	0,64	15,2
4	5,5	5,02	0.48	8,7
5	6,2	6,13	0,07	1,1
6	6,8	6,8	0,0	0
7	7	7,0	0,0	0
8	6,6	6,7	-0,1	-1,5
9	6,0	5,93	0,07	1,1
10	5,0	4,4	0,6	0,12