Теоретический закон распределения. Доверительный интервал, страница 4

Таблица 1.4.

В результате гистограмма и полигон будут иметь следующий вид:

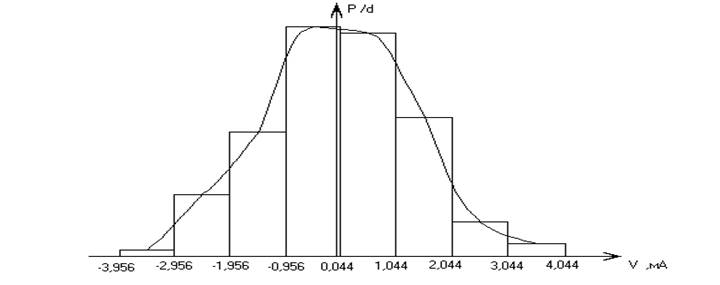
Искомый теоретический закон распределения может быть найден В результате подбора некоторой аналитической функции,соответствующей внешнему виду гистограммы и полигона, с тем, чтобы граффики теоретического и практического закона максимально точно совпадали во всем диапазоне измерений υ.По гистограмме и полигону предположим, что случайная величина υ имеет нормальное распределение, которое описывается законом распределения:

p(υ)= (1/s (2p)^1/2)*e^-0,5(v/s)2

Построим граффик закона распределения p(υ), он будет иметь следующий вид:

  -3.956            -2.956            -1.956          -0.956         0.044              1.044             2.044             3.044               4.044  

Для оценки соответствия практического и теоретического распределения применяют критерий согласия Пирсона. Для этого вычисляют величину χ²=n∑( P_j^*-P_j)²/P_j,

где P_j -вероятность попадения υ в j-й интервал, найденная по теоретическому закону.

P₁ =0,0146 мА       P₃ =0,1558 мА     P₅ =0,2646 мА     P₇ =0,0659 мА

P₂ =0,0562 мА       P₄ =0,2574 мА     P₆ =0,1676 мА     P₈ =0,0176 мА

Чем меньше  χ² ,тем ближе теоретический закон к практическому,граничное значение χ²_гр, разделяющее области принятия и неприятия гипотезы о том , что случайная величина распределена по найденому закону, определяют по таблице критических точек распределения “хи-квадрат”.

Найдем    χ²_гр(α,l),

где    α-уровень значимости.

            l-число степеней свободы, определяемое из выражения

l=N-3, так как это нормальное распределение.

Из таблице критических точек распределения “хи-квадрат” находим χ²_гр(5,0.05)=11.1 .

Найдем  χ².

     χ²=100*((0.01-0.0146)²/0.0146  +(0.07-0.0562)²/0.0562 +          (0.15-0.1558)²/0.1558 +(0.27-0.25.74)²/0.2574+(0.26-0.2646)²/0.2646 +           (0,17-0.1676)²/0.1676+(0.05-0.0659)²/0.659+(0.02-0.0176)²/0.0176)=   =0.9946

χ²=0.9946

Так как   χ² < χ²_гр ,то принимаем гипотезу о том, что закон распределения случайной величины υ нормальный.

Задание 2: Многократные, независимые равноточные измерения ряда параметров электрических сигналов дали результаты, представленные в таблице 2.1. Определить доверительный интервал, между границами которого с доверительной вероятностью P=0,99 находится истинное значение данного параметра, а также относительную квадратичную погрешность результата измерения.

Таблица 2.1

Амплитуда импульса, кВ

0,113;  0,115;  0,118;  0,114;  0,116; 0,117;  0,118;  0,112;  0,112;  0,116; 0,117;  0,110;  0,112;  0,115;  0,117; 0,116;  0,118;  0,112;  0,115

Решение.

Доверительный интервал – интервал, между границами которого с определенной вероятностью находится истинное значение Х_0. Доверительный интервал определяется при интервальной оценке. Задавшись значением доверительной вероятности P при нормальном распределении случайных величин и при числе измерений n<20, находят коэффициент распределения Стьюдента  t_p,n по таблице, а затем и доверительный интервал  ∆_1,2=t_p,nδ_X,