Теоретический закон распределения. Доверительный интервал, страница 6

Ответ: 30%

 Задача 4. Произведены совместные измерения информационных параметров входной неэлектрической (перемещение, мм) и выходной электрической величин  измерительного преобразователя (датчика перемещения) с целью определения его функции преобразования. Результаты эксперимента представлены в таблице 4.1. Найти аналитическое выражение функции преобразования и значения входящих в ее состав числовых параметров интерполяционным методом и методом наименьших квадратов, построить графики двух аппроксимирующих функций совместно с экспериментальными точками, оценить точность аппроксимации тем и другим методами.

Таблица 4.1

xi, мм	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
ti, мс	0,0	2,4	4,2	5,5	6,2	6,8	7,0	6,6	6,0	5,0

По экспериментально полученным данным построим граффик:

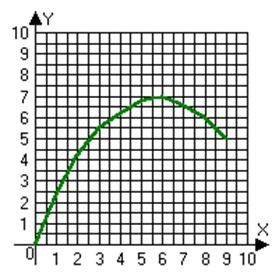
Из графика сделаем предположение (гипотезу) о конкретном виде аппроксимирующей функции f: аппроксимирующая функция - парабола. В общем случае уравнение пораболы имеет вид:  f(x,c1,c2)=c1*sin(c2*x).

Получить аналитическое выражение связи между X и Т можно двумя способами:

1)интерполяционным методом,

2)методом наименьших квадратов.

Интерполяционный метод прост в реализации, но не обеспечивает

Высокой точности аппроксимации всей зависимости в целом. Метод наименьших квадратов обеспечивает наиболее точное решение, но сложнее чем метод интерполяции.

Интерполяционный метод.

Данный метод заключается в составлении системы из k уравнений, неизвестные которых являются числовые параметры:

t_i = f(x_i, c₁, c₂, …, c_k), i = 1,k

В нашем случае  система будет состоять из двух уравнений , неизвестными в которой являются параметры c1,c2.

Для составления системы нужно выбрать две точки, выберем точки: (1,2.4), (2,4.2).

Составим систему:

   c1*sin(c2)=2.4

   c1*sin(2*c2)=4.2

Решая данную систему получим: c1= 4.957 , c2=0.505

Мы получили конкретный вид аппроксиммирующей функции:

t=f(x)=4.957*sin(0.505*x).Найдем значения данной функции в точках x_i  составим таблицу 4.2

Таблица 4.2

Xi, мм	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
ti, мc	0,0	2,4	4,2	4,95	4,47	2,87	0,55	-1,9	-3,88	-4,89