Предел функции в точке. Теорема о единственности предела и об ограниченности функции, имеющей предел. Бесконечно малые величины. Теорема о сумме. Предел функции в точке. Объем тела вращение и площадь поверхности тела вращения. Формула Грина, страница 8

Док-во:Нужно показать Ф’(х)=f(x) xc[a,b]

                                                                              Ф’(х)=f(x)#

Теорема Ньютона-Лейбница:Пусть f(x) непрерывна на [a,b] и F[x]- первообразная

Тогда

Док-во:                                  - первообразная для f(x)

F(x)-Ф(x)=C

  -------       -----------

40.Несобственный интеграл 1-го рода (НИ-I). Признаки сравнения для интегралов от неотрицательных функций.

Определение: Пусть y=f(x) интегрир на [а,b] для любого А

Если                            то он называется НИ I и обозначается

Тогда говорят что интеграл сходится, а если предел бесконечен или не сущ то расходится#

 

                               - сходимость в смысл главного значен

Если расходится хотя бы один в сумме то расходит считается весь интеграл

Признаки сравнения.

1)Признаки срfвнения (непредельная форма)

0≤f(x)≤g(x) xc[a,+]

1)     2) если 1 расход, то 2 расх;если 2 сходится, то 1 сходится

2расход=> 1расход

Признак сравнения (в “предельной” форме)

 

Пусть f(x) и g(x)неоприц на [a,+] и

Тогда    (1)    и  (2)  сходится и расходится одновременно #

док-во(предельного признака):

дано

                           E>0  N(E)>0; x   |x|>N

          

g(x)     (A-E)<f(x)<g(x) (A+E)

Пусть                      сходится=>                      сходится

41.Абсолютная и условная сходимость НИ-I. Признак Дрихле условной сходимости. Примеры.

Опр  (1)                      Если сход интеграл (2)                            то интеграл (1) наз-ся абсолютно сходится

Если (2)расход, а (1) сходится по 1-му условию схожд

(1)                    ----- рассмотрим                   xс[1;+]

(2)                    сходится => (1) сходится абсолютно

Признак Дирихле: пусть |f(x)|≤A x и    

Тогда интеграл сходится условно

42.Несобственные интегралы II-го рода. Связь между НИ-II и I родов.

Несобственный интеграл II рода

Пусть y=f(x) не огранич в окрестности т. b слева [a,b], но                       , то он называется НИ-II от f(x)

Пусть f(x)интег на [a,b] и неогранич в т. сС(a,b)

Е₁ и Е₂ стремится к 0 не одинаково

                  f(x) неограниченна при x->b        t=1/(b-x)- связь между НИ-II и НИ-I

44.Вычисление длин дуг плоских кривых

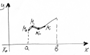
Пусть y=f(x) непрерывна в месте со своей производ на [a,b]

найти длину дуги

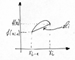
Ломанная                   -длина ломанной                          .   Если                           , то ломанная

(длина) приближает АВ

                                                         ------

 где                           теорема Лагранжа-----

Переходим к lim при Δl→0

                                       длина дуги хорды

 

                                                     #

параметрич случай

 

                    L наз гадкой если x(t), y(t) непрерывно дифференцирован и

----------------------------------------------------------------------------------

         

полярная система координат

               

-----------------

-----------

45.Объем тела вращение и площадь поверхности тела вращения

Объем тела вращения

------

непрер диффер на [a,b]

----------------------

lim при max

 

46. Опр: Пусть  непр на Д c кусочно-гладкой границей. Если    не

 

зависящий от способа разбития Д и выбора точек         то он наз двойным интегралом от до Д обозначается  

 

47 опр: областью Д наз. правильной в направлении OX(OY) если прямая проходящая через любую внутр точку обл Д параллельно OX(OY) пересекает границу области ровно в 2х точках

  Д правильная в напр ОХ и не явл прав в напр ОY

опр: область Д наз прав если Д правильная в направлении ОХ и ОY#

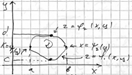 на Д задана непр ф-ия

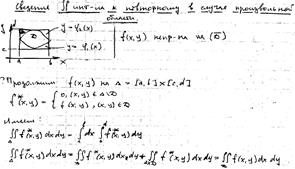
метод вычисления :

 

50.

 

51.

53.формула  Грина