Предел функции в точке. Теорема о единственности предела и об ограниченности функции, имеющей предел. Бесконечно малые величины. Теорема о сумме. Предел функции в точке. Объем тела вращение и площадь поверхности тела вращения. Формула Грина, страница 3

Эквивалентные определение

Опр 2: Если                                     то f(x) называется непрерывной в точке х₀

 

Обозначим:                                                                  -------

Опр3: f(x) называется непрер в точке х₀, если               =

При                                     Функция разрыва

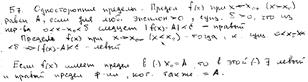
8.Бесконечно большие функции. Связь б.м и б.б величин.

опр f(x)наз-ся б.б. при   x→ х₀   

если                  

упр. Док-ть утверждение

f(x)-б.б при   x→ х₀   <=>                 при x→ х₀   

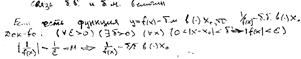
9.Основные теоремы о непрерывных функциях на отрезке(теоремы Вейерштрасса).

теорема 1: пусть f(x) непрерывна на [a,b]

тогда f(x) ограниченна на [a,b]

теорема 2:если f(x) непрерывна на [a,b] то она достигает на нем наибольшее и наименьшее знач

f(x)=x                      (0,1)

                                  sup f(x)=1

                             inf f (x)=0                                                           

теорема 3: если f(x) непрерывна на [a,b] то она принимает на нем любое значение между наименьшем и наибольшем

10.Производная функции в точке. Геометрический и механический смысл.Касательная и нормаль к графику функции.

Определение: Производной функции f(x) в т. х₀ называется                 где                                                                                             ---------

геом смысл производ y=f(x)

                               ------ y’=tg

опред: производ есть tg угла наклона косательной проведение в точке х₀ к f(х₀) графику данной функции

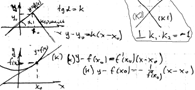(к): y- y₀=k(x- x₀)---(н):  y- y₀=-1/К

­

11.Определение: f(x) наз диффиренцируемой в т. х₀ если ее приращение                                    , где α(x)-б.м при x→ х₀  

Теорема:y=f(x) – диффер в т. х₀ <=> f’(х₀)

Док-во:

                              ----                                          -----    y’(x)=A

 

12.теорема:

пусть f(x) и g(x) дифф-мы в т. х₀ тогда:  a)(f(x)±g(x))’= f’(x)±g’(x)

б)(f(x)*g(x))’= f’(x)*g(x) +g’(x)*f(x)  в)

док-во:

a)y= f(x)±g(x)----Δy=f(х₀+Δx)±g(х₀+Δx)- f(х₀)-g(х₀)=( f(х₀+Δx)- f(х₀)) ±g(х₀+Δx)-g(х₀))

Разделим на Δx, и пусть Δx→0

б)Δy= f(х₀+Δx)* g(х₀+Δx)- f(х₀)g(х₀) -----------y= f(х)g(х)

 

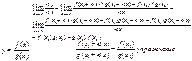С)                  ---------------

теорема( производная сложной функции)

y=g(x)=f(x)-------x=x(t)=φ(t)---------сложная функция у=у(х(t))-------производная

док-во:  функции y(x) и x(t) дифф-ма в т. х₀ и t₀-----Δy=AΔx+α(Δx)Δx

                        

                                                                    Δt→0

y_t’=f’(х₀)x’(t₀)= y_x’* x_t’

13.теорема

пусть y=f(x)монотонна в окр-ти x₀ и f’(x₀), и x’(y₀)-где x=g(x) тогда y’(x)=

Док-во:

Упражнение:

Найти производ:  y=arctgx ----x=tgy----

14. Опред: Дифференцируема функция y=f(x) в т. х₀ наз-ся главная лин. часть приращения функции в данной точке.  dy=f’(х₀) Δx=f’(х₀)dx  покажем что dy – главная часть Δy

                             т.к.            -б.м. при

инвариантность формы дифф-ла

пусть y=y(x), x=x(t)    y=y(x(t))------

геометрический смысл дифф-ла: существование касательной

дифф функции в точке это есть приращение ординаты касательной проведенной к гр. функции в данной точке. При “малых” приращения Δx ----Δy≈dy

формула прибл. Вычисл: f(х₀+ Δx)-f(х₀) ≈f’(х₀) Δx-----f(х₀+ Δx) ≈ f(х₀)+f’(х₀) Δx

15.Дифференцирование функций, заданных параметрически и неявно.

неявные функции

F(x,y)=0 ----                      -----                             --------ln(y)=g(x)lnf(x)

диффен  равенство

                                                       -------

Производная параметрические заданной фун-ии:                  α<t<β

считаем, что t=t(x), тогда y=y(t(x))