Предел функции в точке. Теорема о единственности предела и об ограниченности функции, имеющей предел. Бесконечно малые величины. Теорема о сумме. Предел функции в точке. Объем тела вращение и площадь поверхности тела вращения. Формула Грина, страница 7

Опр. Неопределенный интеграл от функции f(x) называется совокупность первообразных

Основные свойства интеграла (неопр)

1)

2)                                            3) f(x)dx=dF(x)          

I Интегрирование по частям

Теорема: пусть функция U(x) иV(x) непрерывна дифференцирована

Тогда                                     или

Док-во

(u(x)*v(x))’=u’(x)*v(x)+u(x)*v’(x)----------u(x)*v’(x)=(u(x)*v(x))’-u’(x)*v(x)

         #

­

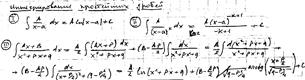
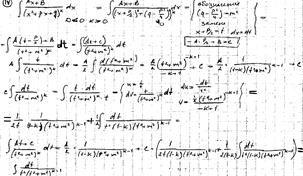
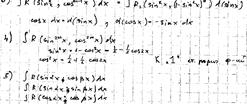
36.Интегрирование иррациональных выражений

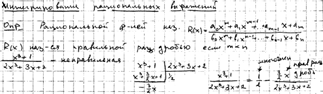
I Рац. функции   II тригонометрические       III иррациональные

теорема: рац функции интегрируемы в элементарной функции:

многочлен;рациональная дробь; неправ дробь→ многочлен+правтльная дробь

многочлен интегрируем

правильная рациональная дробь разлог в сумму простейших дробей

тригонометрия: теорема: функции вида R(cosx, sinx) интегрируема в виде элементарной функции

док-во:

             -------                                    --------

по предыдущей теореме док-но

1)  дробно-линейная иррациональность R(x,(               ,…,                 ))

Функции данного класса интегрир-мы в элементарных

Док-во

Замена                      где

                       -----                                         

 

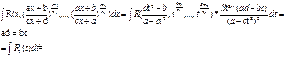
Частный случай

                                                                  x=t²  ,

Квадратичная иррациональность

А) Пусть Если D=0 то 1 корень х, и =>

Если D>0=> 2 действительных корня x₁ и x₂

-дробно лин иррациональность

B) D<0 прочитать подстановки Эйлера

      

37.Пусть y=f(x) непрерывна на [a,b] и пусть f(x) неотрицателен на [a,b]

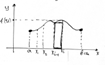
Разобьем [a,b] на n частей

 

обозначим                                                выберем точки

f(     )        -площадь прямоуг

Составим

Рассмотрим предел                                                      не зависящий от выбора ζ

Тогда он наз-ся определенным интегралом от f(x) на [a,b] и обозначается

Классы интегрируемых (по Риману) функций:

I  Непрерывные на отрезке функции

II  Ограниченные на отрезке функции имеющие конечное чило точек разрыва

Основные свойства определенного интеграла

Пусть f(x) и g(x) ентегрируемы на [a,b]

I с-константы

II

 

Док-во:

 

III

A)  Пусть a<c<b

Переход к

В)  Пусть a<b<c

1)

2)

3)

Использовалось при доказательстве

4) Если f(x)≥0 хс[a,b], то

доказательство                           f(ζ_i)≥0  i   Δx_i>0      тогда сумма ≥0

5)Пусть f(x)≤g(x) хс[a,b]

Тогда

Док-во:Рассмотрим f(x)-g(x)≤0. Тогда

6)

док-во:    -|f(x)|≤f(x)≤|f(x)|

7) Пусть m и M соотв наименьшее и наибольшее значение f(x) на [a,b] тогда

док-во:

m≤f(x)≤M, xc[a,b]

38.Пусть y=f(x) непрерывна на [a,b] и пусть f(x) неотрицателен на [a,b]

Разобьем [a,b] на n частей

 обозначим  выберем точки

f()-площадь прямоуг

Составим

Рассмотрим предел                                                              не зависящий от выбора ζ

Тогда он наз-ся определенным интегралом от f(x) на [a,b] и обозначается

Теорема о среднем:Пусть y=f(x) непрерывна на [a,b].Тогда ζс(a,b), что

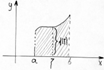
док-во:в силу непрерывности f(x) по теореме Вейерштрассе f(x) достигает на [a,b] наибольшее (М) и наименьшее (m) значение

     По теореме Вейерштрасса ζс(a,b)

Интегрирование по частям:Пусть u(x) и v(x) непрерывно дифф-мы на [a,b] тогда

док-во: (как неопр интеграл)

замена переменной в опред интеграле:пусть f(x) непрер дифферен на [α,β], где a=φ(α), b= φ(β) и φ(t) монотонная на [α,β]

Тогда

Док-во:F(x)-первообразная для f(x)

-----

                                                                                =F(b)-F(a)

38.Интеграл с переменным верхним пределом

Теорема: Функция Ф(х) есть первообразная на f(x)на [a,b]