Предел функции в точке. Теорема о единственности предела и об ограниченности функции, имеющей предел. Бесконечно малые величины. Теорема о сумме. Предел функции в точке. Объем тела вращение и площадь поверхности тела вращения. Формула Грина, страница 6

                                                                 (-лежит м/у       и                , -лежит м/у      и

                )

26. Теорема (производ сложно функции)

Пусть z=f(x,y)  дифф-ма в т.                 и пусть x=x(u,v) дифф в т.                а y=y(u,v) дифф-ма также в т.             .  Тогда z=z(x(u,v),y(u,v)) дифф-ма в т.                и имеет место формулы

Часные случаи-----------------z=z(x,y), x=x(t)y, y=y(t)

                                               --------z=z(x,y), y=y(x)

 

док-во (теорема  о дифф сложной ф-ии):    z(x,y) -дифф в точке 

                                                               ---------

 при    

 

                                                     --------

                                                      

 

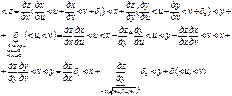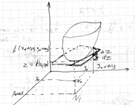 27.Касат пл-ть и нормаль к поверхности

Плоскость наз-ся касательной к поверхности в т.        , если касательная к любой кривой на поверх, проходящ через т.          лежит в плоскости #

При малых  и           

 

                                                                                                                #

Случай неявного задания поверх

          

               

                                                                             --------

В случае

                                                          

геометрический смысл: существует касательная плоскость

28.Произв неявно зад ф-ции

---------

------                  ---------

                         частное

------   

                                                      ------

   -----

                                                              произ неявно зад функ

дополнение к неявно зад ф-ии : Пусть

29.

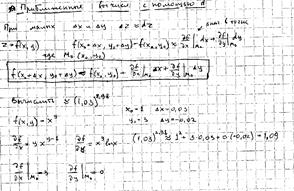
Опред: Функция z=f(x,y)  наз-ся  дифференцируемой в т. если  где А и В не зависит от и

α и β – б.м. при  и

30. Производные  высших порядков

Пусть                        имеет части произв                 если         и       является дифф, то можно

определить вторые частные производные

                            

теорема (o равенстве смешанный производ)

Пусть  y функ                         в точке                 существуют все производ 2-го порядка вкл и смеш производ непр в точке                  тогда они равны

31.Экстремумы ф-ии нескольких переменных

Для n=2

Опр. Точка                       из области опред. функции                          наз. т. локального максимума (лок мининума) ф-ии                  если                   , такая, что

                               -----

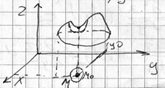  для любой

т. Лок макс и мин –наз точками экстремумов

Необходим усл экстрем

Пусть                      - т. экстремум                        Тогда либо        и        равны 0, в т.       либо не в т.

Пусть                          и                          рассмотрим                                        y=const

Для               т.       есть т. экстрем тогда                                    

                    для         аналогично

32.теор.(достаточные условия экстрем)

пусть т.                      стац т. функ                        тогда если AC-B²>0, то т.         - т. экстремума функции, а именно т лок макс если A<0

        не явл экстр если AC-B²<0. случай AC-B²=0 треб дополнит исследования

Нахождение наибольшего и наим значения                         на замкнутой огран области

      Г-граница

Порядок исследования

1)  ищем точки из Д, удовлетв усл

2)  подставляем                 ”связь” х и у на границе и ищем т. возм экстремума

3)  вычисляем знач функции во всех найденных точках и в точках “склейки”

33.Опр. Функция F(x) называется первообразной для f(x)на (a.b), если F’(x)=f(x)хс(a,b)