Метод прогонки, страница 5

3.3 Задание.

Необходимо решить СЛАУ, у которой матрица коэффициентов имеет трехдиагональный вид, методом правой прогонки. Все результаты численных экспериментов свести в таблицу.

Сделать выводы. Оформить отчет по лабораторной работе.

3.4 Порядок выполнения работы на компьютере.

Войти в MathCAD, для этого нужно набрать:

         Имя пользователя:       Vmstudent

         Пароль:                        student

         Вход в:                         VM

После входа в систему запустить MathCAD 2000 Professional.

Порядок выполнения работы.

Зададим элементы трех диагоналей матрицы acb согласно варианту

                              

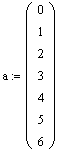
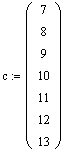
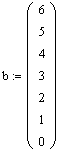
Найдем число элементов в главной диагонали (оно совпадает с числом уравнений в системе) и определим счетчики столбцов с трок

Рассчитаем значения всех членов матрицы acb

Проверим правильность получения  матрицы acb (должно быть только три диагонали)

Зададим столбец свободных членов согласно варианту

Проверка условия диагонального преобладания для полученной матрицы acb (если kn-1 = 0, то условие выполняется )

             

Рассчитаем значения коэффициентов a

Рассчитаем значения коэффициентов b

Рассчитаем значение последнего неизвестного системы уравнений

Зададим счетчик для обратного хода

Рассчитаем найдем все оставшиеся неизвестные системы уравнений

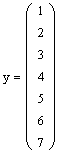
3.5 Содержание отчета.

1.Отчет должен содержать матрицу abc, а также столбец свободных членов.

2.Условие устойчивости метода прогонки.

3.Формулы для расчета коэффициентов  и .

4.Матрицы коэффициентов  и .

5.Формулу расчета последнего неизвестного СЛАУ.

6.Формулу расчета оставшихся неизвестных СЛАУ неизвестных.

7.Матрицу решения СЛАУ.

3.6. Контрольные вопросы.