Метод прогонки, страница 2

Коэффициенты , ,  называются прогоночными.

Если коэффициенты  и  известны, а также известно  то, двигаясь справа налево (от  к ) последовательно определяем все . Задача нахождения ,  по формулам (3.4), (3.5) решается слева направо (от  к ). Начальные значения прогоночных коэффициентов ,  можно определить следующим образом. Полагаем в формуле (2.20) , имеем , а из первого уравнения (2.19) , откуда

          .                                                         (3.6)

Значение  определяется следующим образом. Полагаем в формуле (2.20) , имеем , а из последнего уравнения (2.19)  откуда

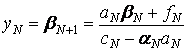.                                              (3.7)

Расчетные формулы (3.3) - (3.7) можно получить также из (3.1), если применить метод исключения Гаусса. Прямой ход метода заключается в том, что на первом шаге из всех уравнений системы (3.1) при помощи первого уравнения исключается , затем из преобразованных уравнений для  при помощи уравнения, соответствующего , исключается  и т.д. В результате получим одно уравнение относительно . На этом прямой ход метода прогонки заканчивается. На обратном ходе для  находятся .

Порядок счета в методе прогонки следующий:

исходя из значений , , вычисленных по формулам (3.6), все остальные коэффициенты ,  для  определяются последовательно по формулам (3.4) и (3.5);

исходя из значения , рассчитанного по формуле (3.7), все остальные неизвестные ,  определяются последовательно по формуле (2.20).

Изложенный метод поэтому называется правой прогонкой.

Аналогично выводятся формулы левой прогонки:

,          ,    ;                               (3.8)

,         ,   ;                               (3.9)