Метод прогонки, страница 4

(3.11)

Вычитая из (3.11) значение по формуле (3.3) имеем для погрешности с заданным . Отсюда ясно, что если по модулю больше единицы, и если достаточно велико, то вычисленное значение будет значительно отличаться от искомого решения . В этом случае говорят, что алгоритм прогонки неустойчив.

Определение. Алгоритм прогонки называется устойчивым, если , .

Условия корректности и устойчивости алгоритма правой прогонки определяются следующей теоремой.

Теорема. Пусть коэффициенты системы (3.1) действительны и удовлетворяют условиям:

, ; (3.12)

, (3.13)

причем хотя бы в одном из неравенств (3.12) и (3.13) выполняется строгое неравенство, т.е. матрица имеет диагональное преобладание. Тогда для алгоритма (3.3)-(3.7) имеют место неравенства: , , , т.е. алгоритм метода правой прогонки корректен и устойчив.

Условия теоремы (3.12) и (3.13) обеспечивают также корректность и устойчивость алгоритмов левой и встречных прогонок. Эти условия сохраняются и для случая системы (3.1) с комплексными коэффициентами , , .

Легко показать, что при выполнении условий теоремы (3.12)-(3.13) система (3.1) имеет единственное решение при любой правой части. Действительно, непосредственно проверкой легко убедиться в том, что матрица представляется в виде произведения двух треугольных матриц и ,

Где

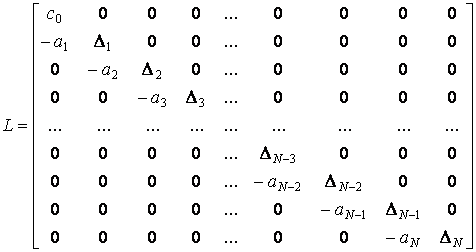
и . Так как

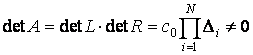
в силу выполнения условий теоремы система (3.1) имеет единственное решение при любых ее правых частях.

3.2 Варианты заданий

Вар.	a	c	b	f
1	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	37, 62, 89, 118, 149, 182, 217, 254, 293, 334, 377, 422, 469
2	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	50, 88, 128, 170, 214, 260, 308, 358, 410, 464, 520, 578, 638
3	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	62, 88, 116, 146, 178, 212, 248, 286, 326, 368, 412, 458, 506
4	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	88, 127, 168, 211, 256, 303, 352, 403, 456, 511, 568, 627, 688
5	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	87, 114, 143, 174, 207, 242, 279, 318, 359, 402, 447, 494, 543
6	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	126, 166, 208, 252, 298, 346, 396, 448, 502, 558, 616, 676, 738
7	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	112, 140, 170, 202, 236, 272, 310, 350, 392, 436, 482, 530, 580
8	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	164, 205, 248, 293, 340, 389, 440, 493, 548, 605, 664, 725, 788
9	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	137, 166, 197, 230, 265, 302, 341, 382, 425, 470, 517, 566, 617
10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	202, 244, 288, 334, 382, 432, 484, 538, 594, 652, 712, 774, 838
11	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	162, 192, 224, 258, 294, 332, 372, 414, 458, 504, 552, 602, 654
12	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	240, 283, 328, 375, 424, 475. 528, 583, 640, 699, 760, 823, 888
13	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25	187, 218, 251, 286, 323, 362, 403, 446, 491, 538, 587, 638, 691
14	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12	12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0	26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38	278, 322, 368, 416, 466, 518, 572, 628, 686, 746, 808, 872, 938

1 2 3 4 5 6

Скачать файл