Метод прогонки, страница 3

, , .                             (3.10)

Здесь  находятся последовательно для значений ; ход вычислений - слева направо.

В случае, если необходимо найти только одно неизвестное, например,   или группу идущих подряд неизвестных, целесообразно комбинировать правую и левую прогонки. При этом получается метод встречных прогонок.

Получим расчетные формулы метода встречных прогонок. Пусть , по формулам (3.4), (3.5), (3.8), (3.9) найдем прогоночные коэффициенты ;,а также ;. По формулам (3.3) и (3.10) при  найдем

откуда определяем

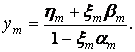
С помощью  по формулам (3.3) последовательно находятся  с помощью формулы (3.10) последовательно находятся

Формулы метода встречных прогонок имеют вид

для прогоночных коэффициентов и

для определения решения.

Произведем подсчет числа арифметических действий для метода правой прогонки. Анализ формул (3.3)-(3.7) показывает, что общее число арифметических операций есть . Коэффициенты  не зависят от правой части СЛАУ (2.19) и определяются только элементами , ,  матрицы . Поэтому, если требуется решить серию задач (3.1) с различными правыми частями, то прогоночные коэффициенты  вычисляются только для первой серии. Для каждой последующей серии задач определяются только коэффициенты  и решение , причем используются ранее найденные .

На решение первой из серии задач расходуется  операций, а на решение каждой следующей задачи  операций. Число арифметических операций, необходимое для решения СЛАУ (3.1) методом левой прогонки и методом встречных прогонок такое же, т.е. .

Метод правой прогонки будем называть корректным, если  при .

Решение  находится по рекуррентной формуле (3.3). Эта формула может порождать накопление ошибок округления результатов арифметических операций. Пусть прогоночные коэффициенты  и  найдены точно, а при вычислении  допущена ошибка , т.е. . При вычислениях с помощью формулы (3.3) мы получаем