Решаем квадратное уравнение и приводим его к виду:
Найдём корни данного уравнения:
Получили новый вид выражения (12):
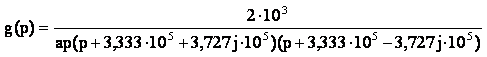(13)
Оригинал 
будем
искать с помощью теории вычетов.
Выражение (12) имеет три полюса, следовательно будем искать три вычета:
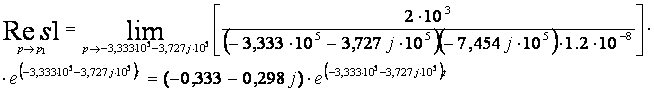
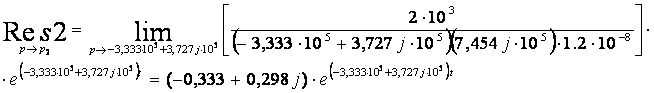
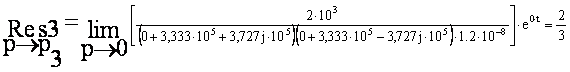
Из теории вычетов известно, что сумма этих вычетов, приведенных выше, будет являться оригиналом:
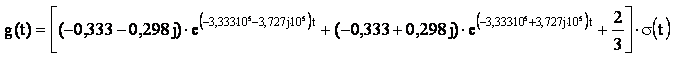
С помощью программы MathCAD построим график конечного выражения и представим его на рисунке 16:
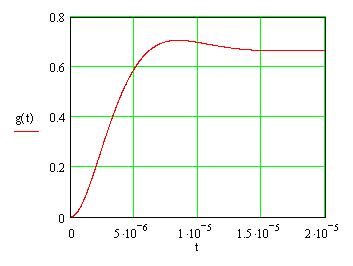
Рис. 16 График переходного процесса данной цепи.
Найдем импульсную характеристику
цепи 
:
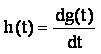
Тогда получаем:
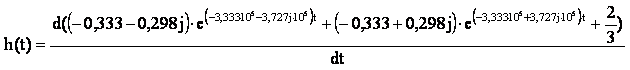
Окончательно:
h(t)=(-0,333-0,298j)·(-3,333·105-3,727j·105)·e(-3,333·100000-3,727j·100000)t + (-0,333+0,298j)·
·(-3,333·105+3,727j·105)·e(-3,333·100000-3,727j·100000)t (14)
С помощью программы MathCAD построим график выражения (14) и представим его на рисунке 17:
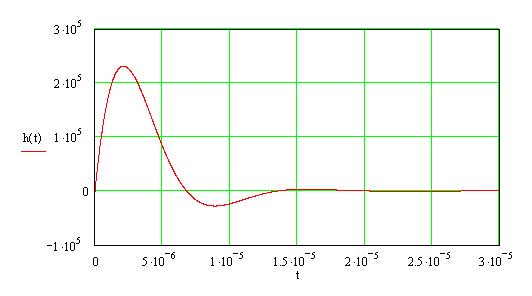
Рис. 17 График импульсной характеристики данной цепи.
4.Спектр выходного сигнала.
Основная формула спектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и на выходе выглядит следующим образом:
Из формулы для нахождения коэффициента передачи запишем:
Следовательно, получаем:
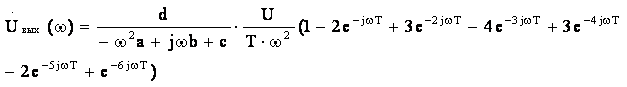(15)
Для нахождения амплитудного спектра выходного сигнала необходимо найти модуль комплексного выражения (15). Разобьём его на два и преобразуем каждую часть по отдельности.
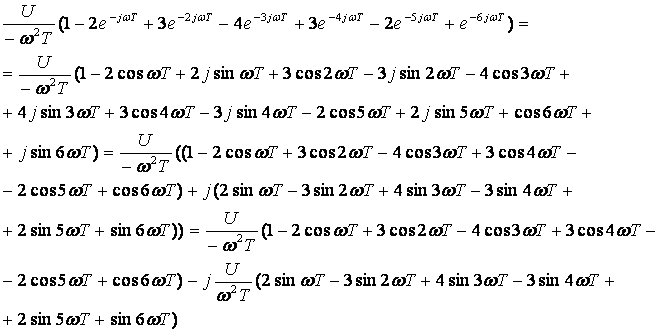
Подставим полученные выражения в равенство (15):
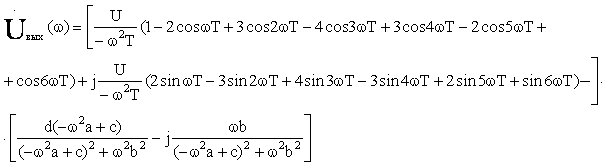
Окончательно получим:
Фазовый спектр выходного сигнала будем искать следующим образом:
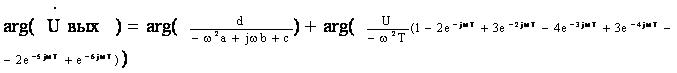
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.