Исследование входного сигнала, страница 5

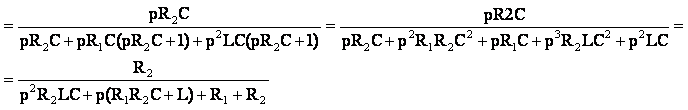
Для упрощения решения произведем замену:

; ;     ;

Выражение для коэффициента передачи примет вид:

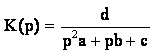                                                                                                        (7)

Заменяем в формуле (7) оператор р на j, получаем:

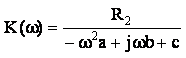                                                                                                 (8)

По данной формуле определяем амплитудно-частотную и фазо-частотную характеристики.

  Запишем выражение для амплитудно-частотной характеристики цепи:

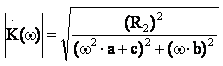
На рисунке 13 приведен график амплитудно-частотной характеристики, сделанный с помощью программы MathCAD:

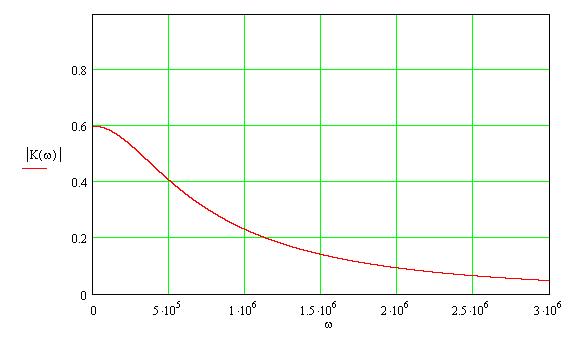
                            Рис. 13 График амплитудно-частотной характеристики.

Рассчитаем фазо-частотную характеристику цепи, учитывая выражение (8):

                                                                                      

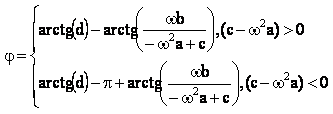                                                                                                                                                                                                                                                (9)

С помощью программы MathCAD построим график выражения (9) и представим его на рисунке 14:

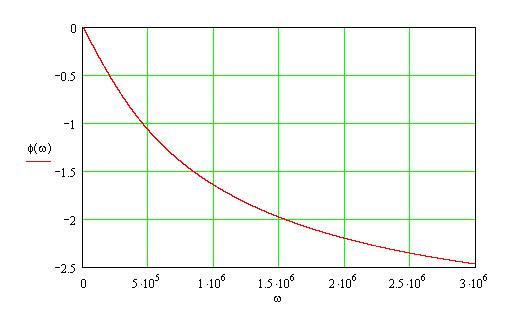
                                 Рис.14 График фазо-частотной характеристики.

3. Импульсная и переходная характеристики цепи.

Переходной характеристикой цепи является реакция цепи на выходе при воздействии на неё сигнала вида , где -единичная функция. Графически этот сигнал представлен на рисунке 15:

                  

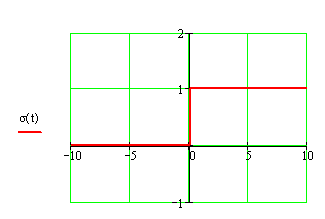
                          Рис. 15 Изображение ступенчатого входного сигнала.

Обозначим переходную характеристику через . Сначала найдём изображение переходной характеристики , далее с помощью обратного преобразования Лапласа, найдём оригинал .

По известному методу, который позволяет найти как произведение К(р) на U_вх(р), запишем:

                                                                                                       (10)

где 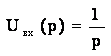-является изображением ступенчатой функции, тогда

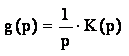                                                                                                            (11) Воспользовавшись формулой  для коэффициента передачи, формула (11) примет вид:

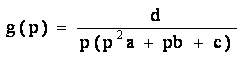                                                                                   (12)