![]() (3)
(3)
Входной сигнал по формуле (3) имеет следующий вид, представленный на рисунке 7:
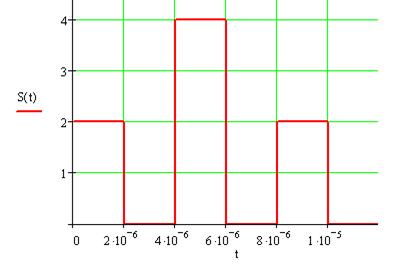
Рис. 7 График входного сигнала.
Для определения спектральной плотности выполним необходимые преобразования.
Преобразуем данную формулу (3) в операторный вид, используя теорему запаздывания:
![]()
При этом изображение простого сигнала определяются как:
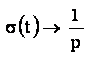
Тогда получаем
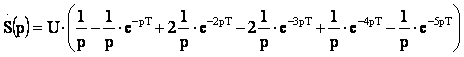 (4)
(4)
В формуле (4) заменяем оператор р на jω (оператор Лапласа) и выносим за скобки, получаем:
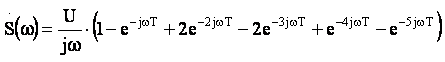 (5)
(5)
Для получения формулы для спектральной плотности преобразуем формулу (5):
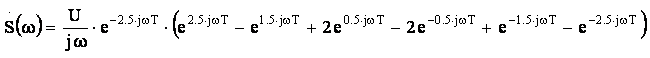
Используем формулу Эйлера для синуса:
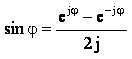
проведем последние преобразования для конечной формулы спектральной плотности:
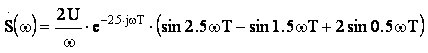 (6)
(6)
1.3. Амплитудный спектр входного сигнала.
Амплитудным спектром входного сигнала является модуль выражения (6) для спектральной плотности
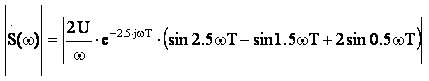
На рисунке 8 приведен амплитудный спектр входного сигнала:
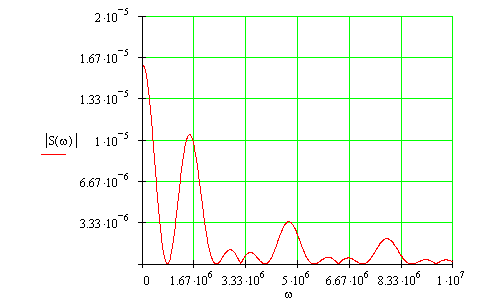
Рис. 8 Амплитудный спектр входного сигнала.
Определим графически ширину спектра.
Для этого проведём горизонтальный уровень ![]() .
Ширина спектра приблизительно равна:
.
Ширина спектра приблизительно равна:
![]()
1.4. Фазовый спектр входного сигнала.
Фазовый спектром входного сигнала является аргумент выражения (6) спектральной плотности:
![]()
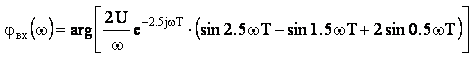
На рисунке 9 представлен фазовый спектр входного сигнала:
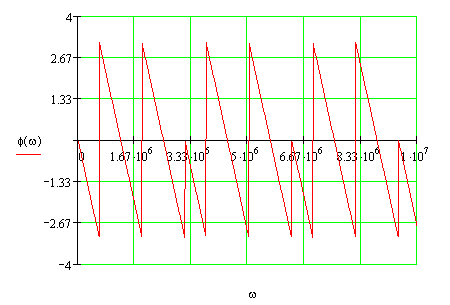
Рис. 9 Фазовый спектр входного сигнала.
2. Частотный коэффициент передачи цепи.
Исходная схема представлена на рисунке 10:
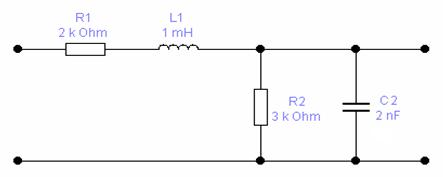
Рис. 10 Исходная схема.
Представим исходную схему в операторной форме:
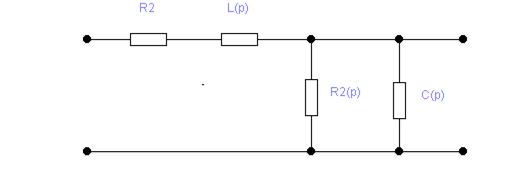
Рис. 11 Исходная схема в операторной форме.
Запишем выражения для элементов цепи в операторной форме:
![]() ;
; ![]() ;
; ![]() ;
;
![]()
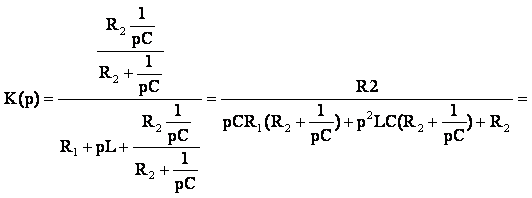
Частотный коэффициент передачицепи определяется отношением напряжения на выходе цепи к напряжению на входе:
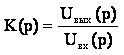
Для нахождения коэффициента передачи цепи преобразуем её к эквивалентной цепи, показанной на рисунке 12:
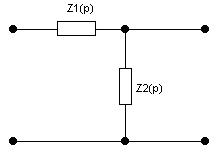
Рис. 12 Эквивалентная схема цепи.
Тогда 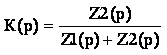
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.