Исследование входного сигнала, страница 3

1. Анализ входного сигнала

1.1.  Корреляционная функция входного сигнала.

Важнейшей временной характеристикой является автокорреляционная функция (АКФ), позволяющая судить о степени связи (корреляции) сигнала и его смещенной во времени копии. АКФ равна скалярному произведению сигнала и копии.

Следовательно, автокорреляционная функция входного детерминированного сигнала S(t) определяется следующим выражением:

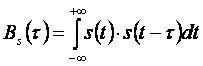
Из которого видно, что сигнал перемножается со своей копией, где τ – интервал смещения сигнала.

Входной сигнала имеет вид:

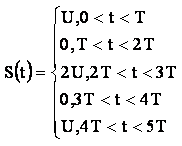                                                                                                          (1)

Рассмотрим функцию корреляции на интервале (0;5Т), зная что вся данная функция будет складываться из суммы  корреляционных функции на каждом из интервалов.

1.1.1.  Смещение при  τ Î (0;Т) имеет вид:

Рис.1 Сигнал и его смещенная копия на первом интервале.

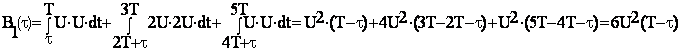
1.1.2.  Смещение при  τ Î (T;2Т) имеет вид:

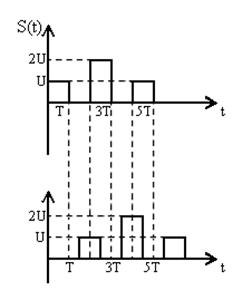
Рис.2 Сигнал и его смещенная копия на втором интервале.

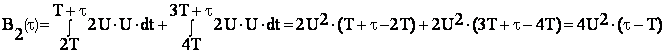
1.1.3.  Смещение при  τ Î (2T;3Т) имеет вид:

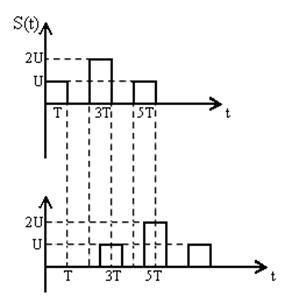
Рис.3 Сигнал и его смещенная копия на третьем интервале.

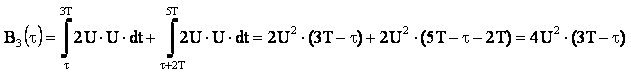
1.1.4. Смещение при  τ Î (3T;4Т) имеет вид:

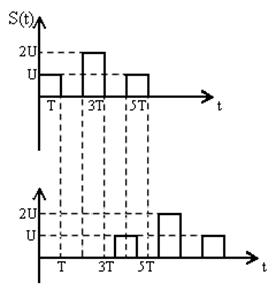
Рис.4 Сигнал и его смещенная копия на четвертом интервале.

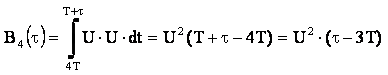
1.1.5. Смещение при  τ Î (4T;5Т) имеет вид:

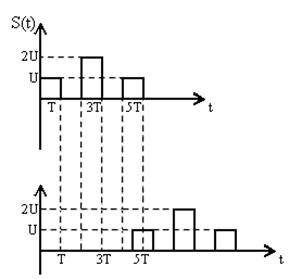
Рис.5 Сигнал и его смещенная копия на пятом интервале.

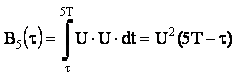
В итоге получаем, что функция корреляции будет иметь вид:

                  

Используя пакет MathCAD, построим график полученного выражения, и представим его на рисунке 6:

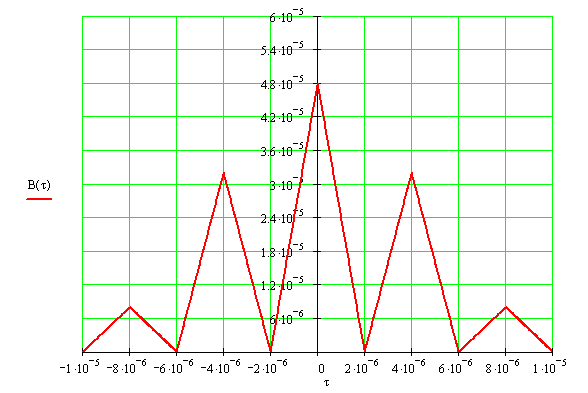
Рис. 6 График корреляционной функции.

Интервал корреляции – это промежуток времени, на протяжении которого можно предсказать поведение функции из условий поведения её в прошлом.  

Найдем интервал корреляции по формуле:

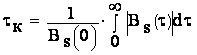                                                                                                       (2) 

С помощью MathCAD найдем последовательно все необходимые значения:

  и

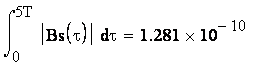
Итак, интервал корреляции, по формуле (2), равен:

τ_к=2.669·10^-6 с.

1.2.  Спектр входного сигнала.

Спектральная плотность– комплекснозначная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе сигнала. Модуль выражения спектральной плотности характеризует амплитудный спектр, а аргумент– фазовый спектр.

В соответствии с формулой (1) запишем динамическое представление входного сигнала: