


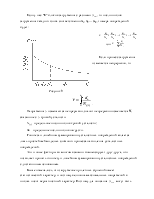



















Режимы нагружения элементов мостов
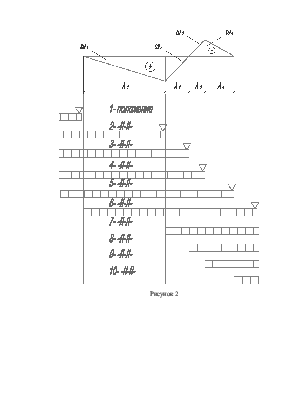
Рассмотрим простейший идеализированный случай – загружение моста полосой равномерной нагрузки. Пусть линия влияния усилия в рассматриваемом сечении имеет вид
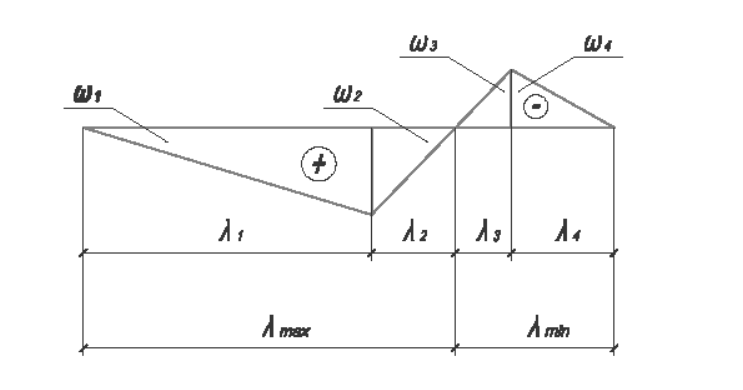
Рисунок 1
Усилие от постоянной нагрузки Sp=pΩp=p∑ω
Усилие от временной нагрузки Sk=kΩk
Рассмотрим
последовательное загружение и разгружение моста равномерной нагрузкой в виде полосы (моделируем движение поезда),
и отложим результаты на графике в системе координат S,T, где T- время 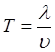 ,
, ![]() -
скорость движения.
-
скорость движения.
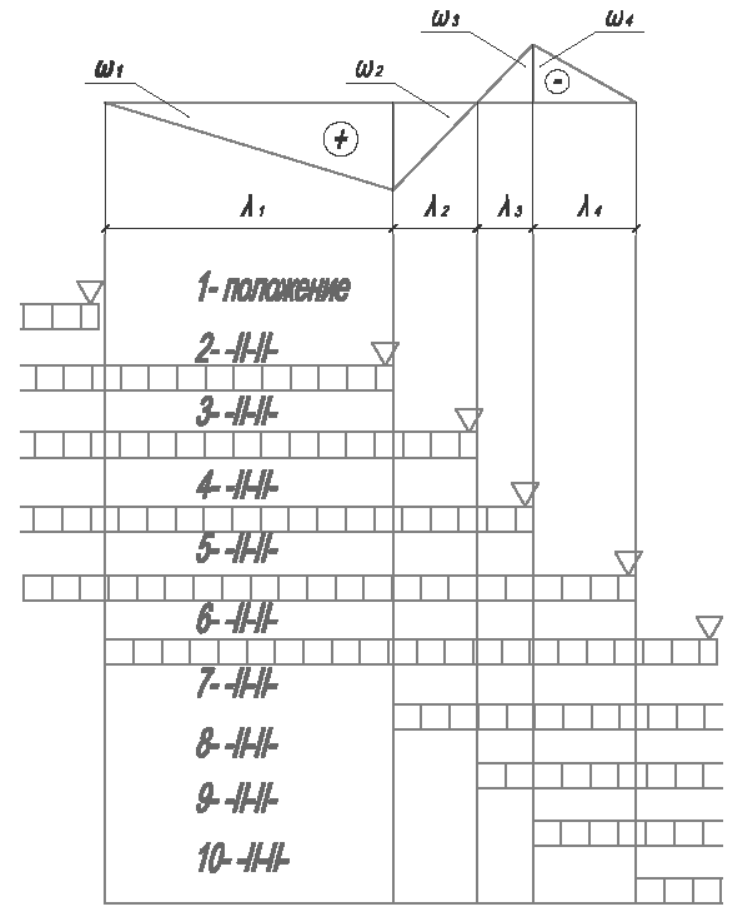
Рисунок 2
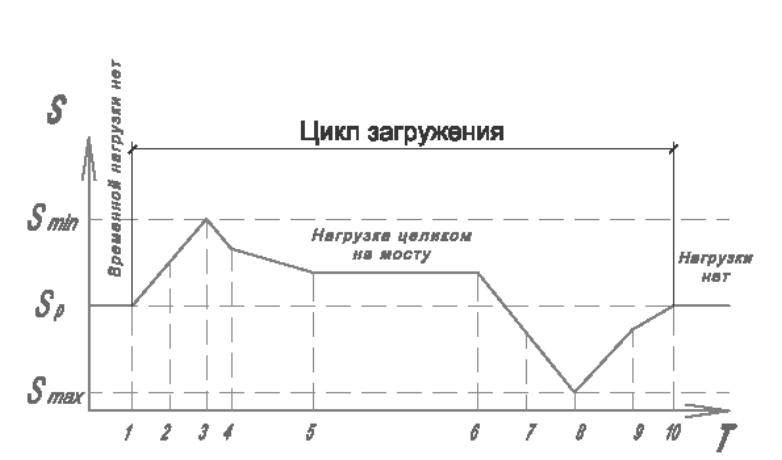
Рисунок 3
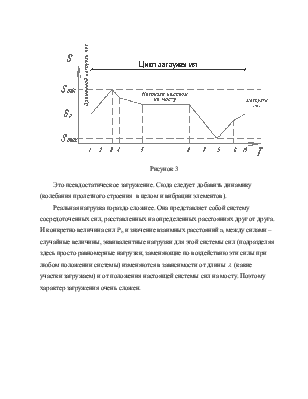
Это псевдостатическое загружение. Сюда следует добавить динамику (колебания пролетного строения в целом и вибрации элементов).
Реальная
нагрузка гораздо сложнее. Она представляет собой систему сосредоточенных сил,
расставленных на определенных расстояниях друг от друга. И конкретно величина
сил Pi, и значение взаимных расстояний ai между силами –
случайные величины, эквивалентные нагрузки для этой системы сил (подразделяя
здесь просто равномерные нагрузки, заменяющие по воздействию эти силы при любом
положении системы) изменяются в зависимости от длины ![]() (какие
участки загружаем) и от положения настоящей системы сил на мосту. Поэтому
характер загружения очень сложен.
(какие
участки загружаем) и от положения настоящей системы сил на мосту. Поэтому
характер загружения очень сложен.
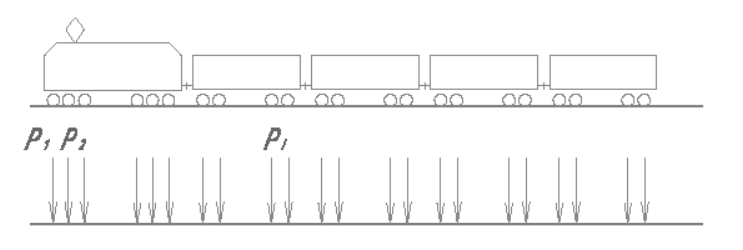
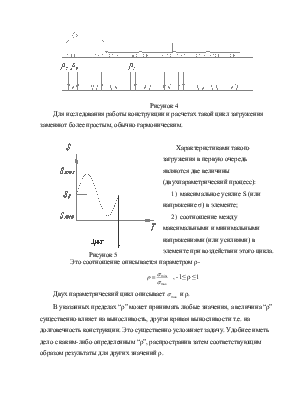
Рисунок 4
![]() Для
исследования работы конструкции и расчетах такой цикл загружения заменяют более
простым, обычно гармоническим.
Для
исследования работы конструкции и расчетах такой цикл загружения заменяют более
простым, обычно гармоническим.
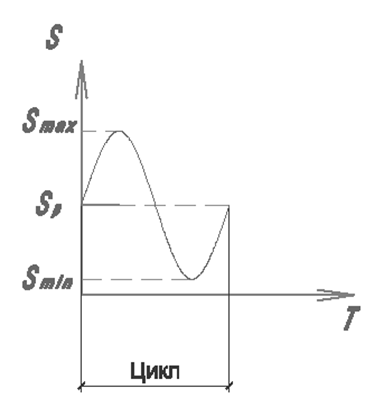
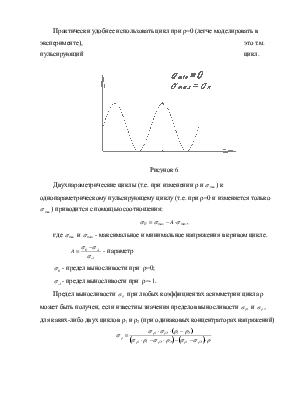
Характеристиками такого загружения в первую очередь являются две величины (двухпараметрический процесс):
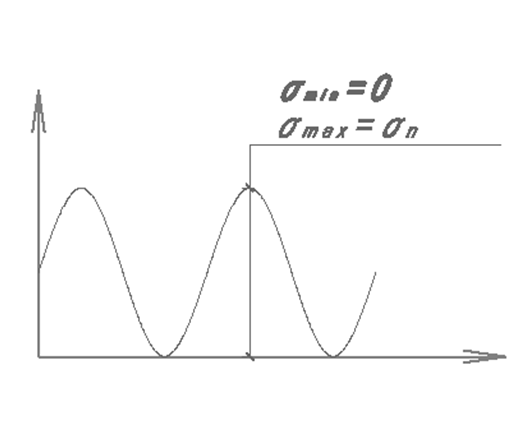
1) максимальное усилие S (или напряжение σ) в элементе;
2) соотношение между максимальными и минимальными напряжениями (или усилиями) в элементе при воздействии этого цикла. Это соотношение описывается параметром ρ-
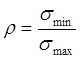
![]() , -1≤ ρ ≤1
, -1≤ ρ ≤1
Двух
параметрический цикл описывает ![]() и ρ.
и ρ.
В указанных пределах “ρ” может принимать любые значения, а величина “ρ” существенно влияет на выносливость, другая кривая выносливости т.е. на долговечность конструкции. Это существенно усложняет задачу. Удобнее иметь дело с каким-либо определенным “ρ”, распространив затем соответствующим образом результаты для других значений ρ.
 Практически
удобнее использовать цикл при ρ=0 (легче моделировать в эксперименте), это т.м.
пульсирующий цикл.
Практически
удобнее использовать цикл при ρ=0 (легче моделировать в эксперименте), это т.м.
пульсирующий цикл.
![]() Двухпараметрические циклы (т.е. при изменении ρ и
Двухпараметрические циклы (т.е. при изменении ρ и ![]() ) к однопараметрическому пульсирующему
циклу (т.е. при ρ=0 и изменяется только
) к однопараметрическому пульсирующему
циклу (т.е. при ρ=0 и изменяется только ![]() )
приводится с помощью соотношения:
)
приводится с помощью соотношения:
![]() ,
,
где ![]() и
и ![]() -
максимальное и минимальное напряжения в кривом цикле.
-
максимальное и минимальное напряжения в кривом цикле.
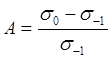 - параметр
- параметр
![]() - предел выносливости при ρ=0;
- предел выносливости при ρ=0;
![]() - предел выносливости при ρ=-1.
- предел выносливости при ρ=-1.
Предел
выносливости ![]() при любых коэффициентах асимметрии цикла ρ
может быть получен, если известны значения пределов выносливости
при любых коэффициентах асимметрии цикла ρ
может быть получен, если известны значения пределов выносливости ![]() и
и ![]() для каких-либо двух циклов ρ1
и ρ2 (при одинаковых концентраторах напряжений)
для каких-либо двух циклов ρ1
и ρ2 (при одинаковых концентраторах напряжений)
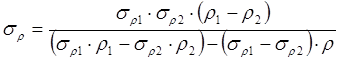
При воздействии на элемент нагрузки, изменяющейся во времени, количество циклов, которые элемент может выдержать до разрушения, определяется кривой выносливости, связывающих число циклов N с максимальным напряжением в цикле. Для каждого ρ – своя кривая выносливости.
![]()
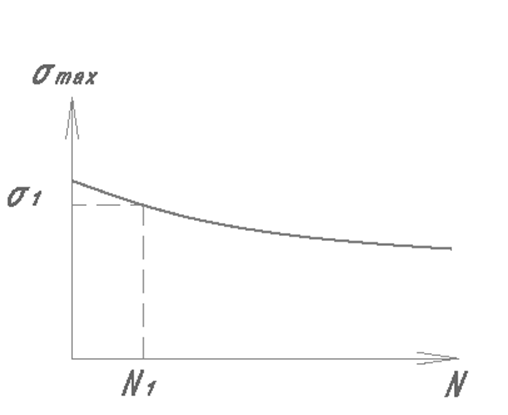
Если при воздействии N циклов элемент (образец) полностью разрушается, то здесь имеет место макроразрушение, то при воздействии меньшего числа циклов в образце (элементе) то же произошли какие-то изменения, разрушения, но степень их такова, что они еще не привели к макроразрушению. Можно считать, что при каждом цикле воздействия в образце (или элементе) происходят какие-то микроповреждения, которые по достижении Nциклов, суммируясь, приводят к полному разрушению материала.
При воздействии переменной нагрузки в элементе возникают микроповреждения, которые суммируясь, образуют макроповреждение с последующим разрушением.
Введем специальную величину ν – меру повреждения, как характеристику тех процессов, которые происходят в материале при воздействии на него изменяющейся во времени нагрузки. Пусть повреждение от i-того цикла характеризуется мерой повреждения νi. Будем считать, что при полном отсутствии повреждений (т.е. до начала эксплуатации) мера повреждений равна нулю, а полному разрушению соответствует значение меры повреждения, равное 1. Тогда, очевидно, можно написать:
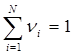 ,
,
где N- предельное число циклов, соответствующих максимальному действующему напряжению (при постоянном значении ρ).
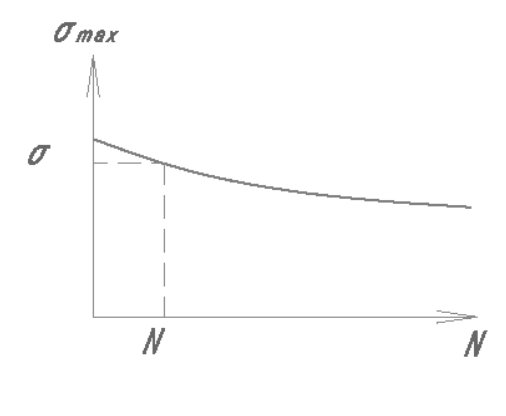
Рисунок 8
Будем считать, что величина νi не зависит от порядка следования циклов, т.е. от местоположения цикла i. Это значит, что νi=const и равняется νi= ν1, где ν1 – просто повреждение от одного цикла нагружения. При этом имеет место равенство:
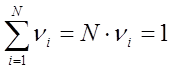
![]() ,
,
откуда 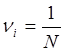 . Это линейная теория накопления
усталостных повреждений.
. Это линейная теория накопления
усталостных повреждений.
При этом, если на элемент воздействует n циклов (причем n<N), то мера повреждения этих циклов будет:
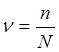 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.