Надежность и долговечность металлических мостов, страница 2

Если у нас “К” блоков загружения с разными , то число циклов загружения каждого блока соответственно n₁, n₂,…,n_K, то мера повреждений будет:

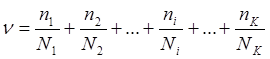или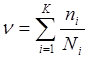

Если процесс загружения изменяется непрерывно, то

.

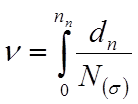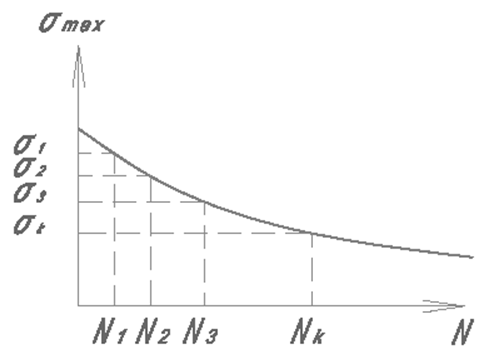
Напряжения σ изменяются непрерывно, значит непрерывно изменяется N, связанное с  σ кривой усталости.

- предельное число циклов кривой усталости;

n_п -  предельное число циклов нагрузки.

Гипотеза о линейном суммировании усталостных повреждений является лишь простейшей моделью сложного процесса накопления усталостных повреждений.

Эти и иные факторы во многом взаимно компенсируют друг друга, что позволяет принять гипотезу о линейном суммировании усталостных повреждений с достаточным основанием.

Выше отмечалось, что загружение пролетных строений имеет статистический характер, и поэтому величина максимальных напряжений в циклах носит вероятностный характер. Поэтому для описания  могут быть использованы характеристики случайной величины, в частности, кривая плотности вероятности f(σ). Начертим ее совместно с кривой усталости.

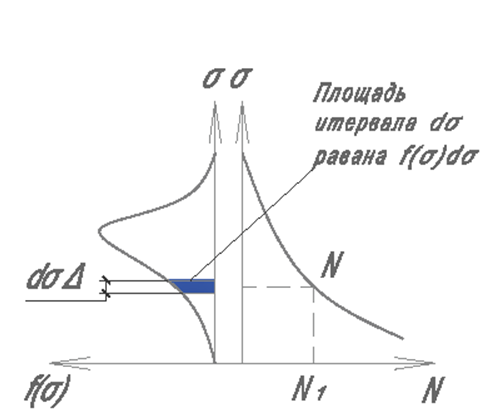
Тогда для интервала ασ число циклов будет:

dn=n₀f(σ)dσ,

где n₀-общее число циклов воздействий (соответствует всей кривой).

Этому dn будет соответствовать свое предельное значение числа циклов N.

После этого мера повреждения будет:

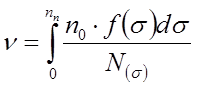
При введении кривой распределения f(σ), как говорилось ранее, пределы изменения  от -∞ до +∞. Кроме того, при σ<σ^{`</sup> , где σ<sup>`}-  некоторое напряжение, накопление усталостных повреждений не происходит. Поэтому пределы интегрирования должны быть откорректированы и выражение для υ принимает вид:

 .

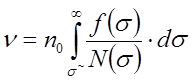Из результатов экспериментов найдено, что кривые выносливости могут быть представлены уравнением σ_i ^mN_i=const,

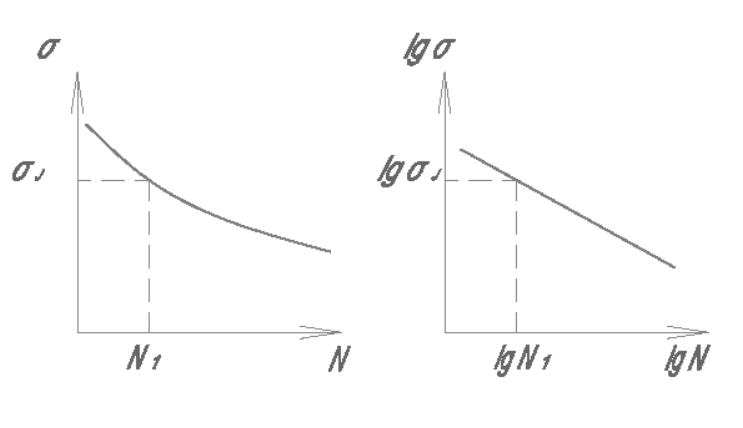
Рисунок 11

где m-некоторый параметр, что приводит к линейной зависимости в логарифмических коэффициентах. Это позволяет перейти от циклов с различными амплитудами σ_i к циклу с заранее выбранной амплитудой σ_э и соответствующим предельным числом циклов N_э. Для этого запишем

σ^m..N= σ_э N_э=const,

откуда .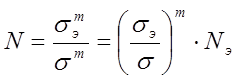

В качестве σ_э можно выбрать любое значение σ>σ̉ (смотри выше определение σ̉).

При назначении σ_э можно, в частности, использовать следующий экспериментальный факт: кривые усталости зависят от концентрации σ, однако кривые усталости (а в логарифмических координатах –прямые) пересекаются в некоторой точке с координатами σ_оп, N_оп.

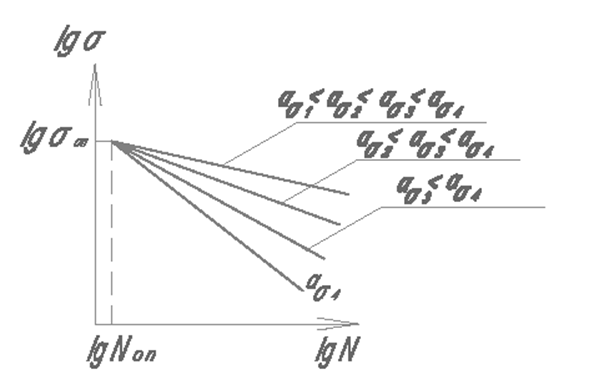
Эти величины и используют в качестве σ_э и N_э. σ_оп и N_оп определяются экспериментально при ρ=0.

При этом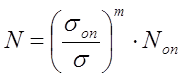

Подставим это N в выражение для ν:

.

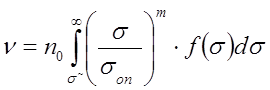т.о. величина меры накопления усталостных повреждений при воздействии n₀ циклов с максимальными напряжениями σ, описываемыми функцией распределения  f(σ), равна:

.

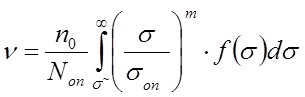Как показывают обследования и испытания эксплуатируемых мостов, величина максимальных напряжений  σ в циклах хорошо согласуется с нормальным законом распределения с функцией плотности вероятности:

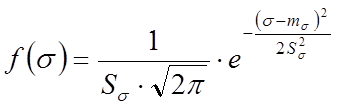
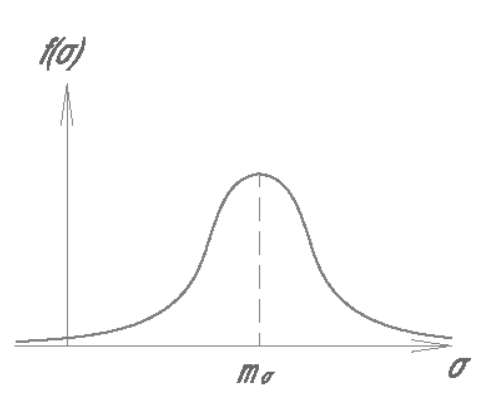
Рисунок 13

После этого

(*)

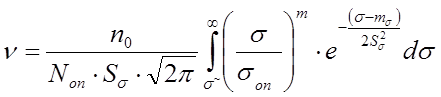Здесь m_σ- математическое ожидание распределения σ;

          S_σ-  средне-квадратчное отклонение  σ.

Критерии оценки надежности и усталостной долговечности

Вероятностное определение предельного значения меры накопления усталостных повреждений.

При накоплении усталостных микроповреждений, в процессе зарождения и развития усталостных макроповреждений (трещин) выход элемента из строя произойдет гораздо быстрее, чем величина меры повреждения ν достигнет единицы. Кроме того, предел выносливости, определяемый по результатам, имеет значительный разброс, и кривая усталости представляет собой кривую математического ожидания зависимости σ от N (и наоборот) с вероятностью (достоверностью) .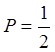

Рисунок 14