Теория химической связи. Гомеополярная связь. Молекула водорода (вариационный метод), страница 5

.                                                                 (6.25)

          С учётом ковалентной составляющей общая волновая функция будет выглядеть следующим образом:

           Y =  Y_ков + С×Y_ион.                                                                               (6.26)

Коэффициент С можно определить вариационным методом из условия минимума энергии системы. Он оказался равным 0.25. С учётом экранировки, поляризации и ионного состояния энергия связи приближается ещё ближе к экспериментальному значения и равна 4.10 эВ.

Лекция 7

6.3 Молекула водорода (вариационный метод).             

Рассмотрим молекулу водорода с позиций вариационного метода на примере волновой функции, состоящей из двух слагаемых:

.

Соответствующая ей энергетическая функция такова:

        Е = 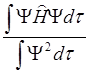 =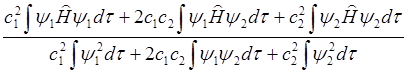.                (6.27)

Введём следующие обозначения:

, , , , .                      

Причём очевидно, что Е₁₂ = Е₂₁ и S₁₂ = S₂₁. Кроме того, если y₁ и y₂ нормированы, то S₁₁ = S₂₂ = 1. Величина Е₁₂ называется недиагональным матричным элементом гамильтониана  относительно функций y₁ и y₂, а S₁₂ называют интегралом перекрывания или интегралом неортогональности.

          Используя принятые обозначения, запишем выражение 6.27 в следующем виде:

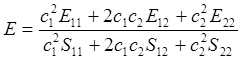                                                                     (6.28)

          Для отыскания коэффициентов с₁ и с₂, согласно вариационному принципу, минимизируем энергетическую функцию Е. Т.е. возьмём частные производные Е по с₁ и с₂ и приравняем их нулю:

                                   dE/dc₁ = 0   и dE/dc₂ = 0.

В результате этого получаем так называемые секулярные (или вековые) уравнения:

;                                                         

Или при обозначении Е₁ = Е₁₁, Е₂ = Е₂₂ и, учитывая, что ВФ нормированы:

;                                                                (6.29)       

.

Если из них исключить соотношение с₁/c₂, то получим:

(Е - Е₁)(Е - Е₂) - (Е₁₂ - Е S₁₂)² = 0.

Корни этого уравнения дают минимальное и максимальное значение энергии системы при равновесном расстоянии между атомами. Эти значения соответствуют основному и возбуждённому состояниям системы. Рассмотрим изменение f(E) при разных значениях Е, где f(E) = (Е - Е₁)(Е - Е₂) - (Н₁₂ - Е S₁₂)².

          Вид зависимости f(E) представлен на рис.6.4.

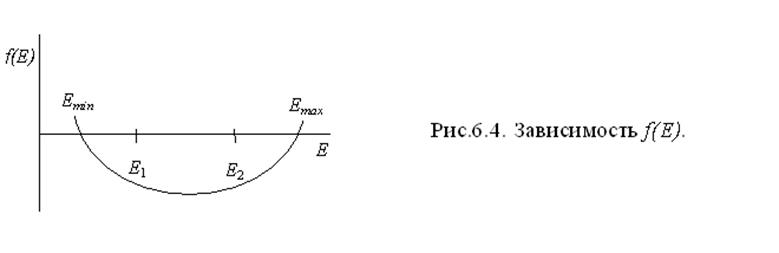Видно, что f(E) = 0 при значениях Е_min < Е₁ и Е_max > Е₂ . Т.е. для линейной комбинации двух волновых функций получаются два уровня энергии, один из которых (основной) ниже, а другой (возбуждённый) выше первоначальных Е₁ и Е₂. Картина получается такой, как если бы два первоначальных уровня Е₁ и Е₂ отталкивались один от другого. При этом такая картина наблюдается не только при равновесном расстоянии между атомами водорода, но и при других значениях R. Даже в том случае, когда кривые Е₁(R) и Е₂(R) пересекаются, кривые, вычисленные для функции Y = y₁ + y₂  (Е_min и Е_max), никогда не пересекаются. Данное правило, которое справедливо и для комбинации из большего, чем две волновые функции, называется  правило непересечения. Правило непересечения было установлено Ландау Л. Д. и Зенером К. в 1932-33 гг. На рис.6.5 данное правило представлено графически. Состояния Е_min (основное состояние) и Е_max  (возбуждённое состояние) важны, поскольку электронные переходы между ними ответственны за одну из характеристических полос поглощения.

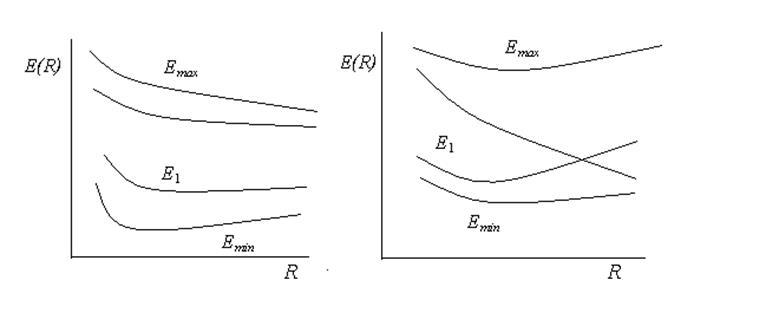
          Рис.6.5. Зависимость Е₁, Е₂, Е_min и Е_max от R.     

          Следует отметить, однако, что правило непересечения справедливо только тогда, когда волновые функции y₁ и y₂ одной симметрии. Потенциальные кривые для волновых функций разной симметрии могут пересекаться.

            6.4. Условия образования химической связи.