Теория химической связи. Гомеополярная связь. Молекула водорода (вариационный метод), страница 2

Здесь  r_1a - расстояние электрона № 1 от ядра “а”. Аналогично для второго атома:

.                                                                                         (6.5)

Зарядовые облака атомов водорода частично перекрываются. Поэтому в качестве волновой функции молекулы водорода следует взять произведение ВФ:

.                                                                                    (6.6)

Т.к. электроны идентичны (неразличимы) справедливым будет и другое произведение ВФ:

.                                                                                    (6.7)

          Как и в случае расчёта атома гелия здесь также необходимо взять симметричную и антисимметричную комбинации исходных волновых функций:

                                                                    (6.8)                

                                                                    (6.8^*)  

Чтобы найти энергию возмущения Е(R), надо взять квадрат волновых функций, умножить на функцию возмущения и проинтегрировать по всем координатам двух электронов. В случае гелия функция возмущения отвечала кулоновскому взаимодействию двух электронов U = e²/r₁₂. Теперь же энергия возмущения, как видно из ур.6.3, будет суммой четырёх пар взаимодействий. Можно использовать и аналогичное выражение для случая обмена электронов местами:

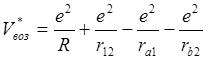.                                                                           (6.3^*)

          Энергия возмущения определяется следующим выражением:

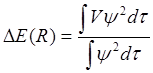.                                                                                     (6.9)

Рассмотрим числитель правой части ур.6.9:

                                                                                                                         (6.10)

Знак ± перед последним слагаемым ур.6.10 отвечает разной симметрии волновых функций ур.6.8. Этот интеграл обозначим буквой А. Два первых интеграла правой части уравнения 6.10 равны между собой и обозначим их буквой С.  Т.о.

С 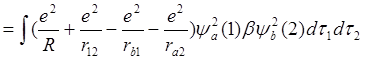                                         (6.11)

            А 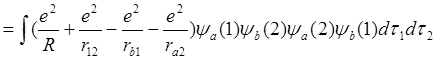.                           (6.12)

Будем считать, что волновые функции каждого из атомов водорода нормированы, т.е.

          .                                                                         (6.13)

Обозначим буквой S следующий интеграл

S.

Тогда  интеграл, стоящий в знаменателе правой части ур. 6.9 (интеграл перекрывания), примет следующее обозначение:

           S².                                                            (6.14)

После принятых нами обозначений выражение 6.9 будет выглядеть следующим образом

DЕ(R) = 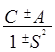.                                                                                     (6.15)

Следует обратить внимание на то, что интеграл С - суть кулоновское взаимодействие, но не классических точечных зарядов, а размазанных электронных облаков с плотностью еY². Другой интеграл, интеграл А – обменный интеграл и характеризует обменную энергию возмущения. Интеграл S² принимает значения от 0 до 1 (в отличие от аналогичного интеграла для атома гелия, где y_a и y_b  ортогональны, т.к. являются ВФ одного атома). S² стремится к нулю при больших расстояниях (R ® µ, зарядовые облака атомов водорода не перекрываются) и равен 1 при R = 0. Т.о. интегралS² играет роль количественной поправки к величине DЕ(R), а при качественном обсуждении им можно пренебречь. Так как при вычислении величины DЕ₊ была использована симметричная орбитальная волновая функция 6.8, то для получения полной ВФ её надо умножить на антисимметричную спиновую ВФ. Поэтому значению DЕ₊ будет соответствовать синглет (основное состояние). Значению DЕ_- будет соответствовать триплет.

          Полная энергия молекулы водорода, отвечающая симметричному и антисимметричному состояниям, соответственно будет такова:

            Синглет     Е₊ = 2Е₀ + 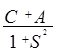 ;                                                         (6.16)

            Триплет      Е_- = 2Е₀ + 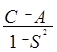 .                                                         (6.17)

          Запишем орбитальные волновые функции для этих двух состояний. После нормировки (условие 6.13 и ) получим следующий результат: