определяется нейтронно-физическими свойствами размножающей системы. Нейтроны, средняя длина свободного пробега которых меньше, чем расстояние, которое им необходимо преодолеть до границы системы, остаются в системе.
Поскольку в критической системе Кэф =1, то
J =1/k¥, (1.3.5)
но из (1.3.3) имеем k¥ = B2L2 +1, следовательно, доля нейтронов, остающихся в системе составит
J= 1/(1+ ![]() L2) (1.3.6)
L2) (1.3.6)
и Кэф теперь можно записать следующим образом:
Кэф= k¥/(1+ M2![]() ).
(1.3.7)
).
(1.3.7)
Здесь параметр ![]() должен
быть связан с геометрическими характеристиками размножающей среды (тогда как k¥ и L2
относятся к материальным характеристикам среды, таким как замедляющие и
поглощающие свойства), его называют геометрическим параметром (см разд. 1.1.2)
должен
быть связан с геометрическими характеристиками размножающей среды (тогда как k¥ и L2
относятся к материальным характеристикам среды, таким как замедляющие и
поглощающие свойства), его называют геометрическим параметром (см разд. 1.1.2)
Подставим (1.3.6) в (1.3.5), получим
k¥/(1+ ![]() L2)=1 (1.3.8)
L2)=1 (1.3.8)
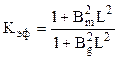 -Но поскольку для критической системы геометрический и
материальный параметры должны быть равны (см разд. 1.1.3), то
-Но поскольку для критической системы геометрический и
материальный параметры должны быть равны (см разд. 1.1.3), то ![]() =
= ![]() =
= ![]() - материальный
параметр среды, отсюда
- материальный
параметр среды, отсюда
(1.3.9)
или, заменив длину диффузии L на длину миграции M, учтя тем самым замедление нейтронов, получим
Кэф = 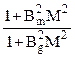 (1.3.10)
(1.3.10)
- одногрупповое уравнение критичности системы.
Соотношение
(1.3.10) позволяет определить Кэф системы,
если имеется информация о геометрических размерах, длине экстраполяции и
свойствах размножающей среды (![]() ). Материальный параметр определяется либо экспериментальным, либо
расчетным путем.
). Материальный параметр определяется либо экспериментальным, либо
расчетным путем.
Произведение
параметров M2![]() равно вероятности нейтронам покинуть систему в расчете на один нейтрон,
поглощенный в размножающей среде. Таким образом, доля нейтронов, теряющихся
вследствие утечки, равна:
равно вероятности нейтронам покинуть систему в расчете на один нейтрон,
поглощенный в размножающей среде. Таким образом, доля нейтронов, теряющихся
вследствие утечки, равна:
1- J = M2![]() / (1+ M2
/ (1+ M2![]() ).
).
Таблица 1.3.3. Одногрупповые плотности потока нейтронов и геометрические параметры для критических реакторов
|
Конфигурация системы |
Плотность потока |
Геометрический параметр, B2g |
|
Бесконечный плоский слой (толщиной а) |
j(x) = Acos(px/a) |
p2/а2, где а - толщина слоя |
|
Сфера (радиусом R) |
|
(p/R)2 |
|
Полусфера (радиусом R) |
[4,49/R]2 |
|
|
Прямоугольный параллелепипед (со сторонами a, b,c,) |
j(x) = A1cos(px/a) j(y) = A2cos(py/b) j(z) = A3cos(pz/c) |
(p/a)2 + (p/b)2 + (p/c)2 |
|
Цилиндр (радиусом R, высотой Н) |
j(r) = A1Jo(2.405r/R) j(z) = A2cos(pz/H) |
(2.405/R)2 + (p/H)2 |
|
Бесконечный цилиндр (радиусом R) |
j(r) = A1Jo(2.405r/R) |
[2,4048/R]2 |
|
Бесконечный полуцилиндр (радиусом R) |
[3,832/R]2 |
Замедлитель уменьшает mкр для делящихся нуклидов (существенный рост sf, см таблицу 7) и увеличивает для n-четных ядер (уменьшение sf, см таблицу 1).
Отражатель - неразмножающая среда, окружающая активную зону и возвращающая часть нейтронов в активную зону, уменьшая тем самым mкр (сопоставление таблиц 2 и 4).
Эффективность отражателя растет почти линейно при малой толщине отражателя, а по мере дальнейшего увеличения толщины достигает насыщения.
Важным
практическим приложением ![]() при оценке критичности является возможность пересчета критической
массы систем различных геометрических форм, основанная на приравнивании
лапласиана.
при оценке критичности является возможность пересчета критической
массы систем различных геометрических форм, основанная на приравнивании
лапласиана.
С помощью выражений для ![]() при одном и том же Кэф можно
определить соответствующие размеры систем в форме шара, цилиндра, пластины и
др. Для этого необходимо знание длины экстраполяции λ, которая означает для реактора
без отражателя расстояние от границы размножающей зоны до поверхности, где обращается
в нуль экстраполированная плотность потока нейтронов. Для реактора с
отражателем эквивалентом длины экстраполяции является эффективная добавка δ,
которая складывается из длины экстраполяции λ и экономии отражателя Δ: d=l+Δ
при одном и том же Кэф можно
определить соответствующие размеры систем в форме шара, цилиндра, пластины и
др. Для этого необходимо знание длины экстраполяции λ, которая означает для реактора
без отражателя расстояние от границы размножающей зоны до поверхности, где обращается
в нуль экстраполированная плотность потока нейтронов. Для реактора с
отражателем эквивалентом длины экстраполяции является эффективная добавка δ,
которая складывается из длины экстраполяции λ и экономии отражателя Δ: d=l+Δ
Для систем, содержащих растворы урана или плутония, λ = 2,5¸2,8 см;
![]() 3,1 ¸ 3,5 см для бесконечного водяного отражателя;
3,1 ¸ 3,5 см для бесконечного водяного отражателя;
Δ =
4 ¸ 4,3 см для бесконечного бетонного отражателя.
Для
систем, содержащих двуокись урана с обогащением 90% по ![]() (плотность 10,96 г.см-3),
(плотность 10,96 г.см-3),
λ = 3,9 ¸ 5,1 см; Δ = 2,8 ¸ 3,1 см.
Таблица 1.3.4 - Толщина сферических отражателей, см
|
Материал отражателя |
Линейный рост эффективности |
Область насыщения |
¥ |
|
Вода |
до 10 |
10 - 30 |
>30 |
|
Графит |
до 50 |
50 - 100 |
>100 |
|
Бетон |
30 - 40 |
>40 |
Пример 1.3.1
Решим задачу для плоского бесконечного реактора толщиной а.
Запишем уравнение (1.3.4) для одного параметра х ![]() , где B2 = (k¥ - 1)/L2 , x =a’/2= (a +2×ls/3)/2
.
, где B2 = (k¥ - 1)/L2 , x =a’/2= (a +2×ls/3)/2
.
Решение ищем в виде линейной комбинации А×cos (Ba’/2)+С×sin (Ba’/2) = 0. Условие j(а’/2)=0 оставляет только A.cos(Ba’/2)=0, решение которого B×a’/2=np/2 (n =1, 3, 5, …), или B = np/a’.
Существует единственное решение при n=1. (k¥-1)/L2 = B2 = (p/a’)2.
![]() Отсюда
экстраполированная толщина должна удовлетворять условию
Отсюда
экстраполированная толщина должна удовлетворять условию
a (1.3.4)
Пример. 1.3.2.
Найти критическое соотношение между атомами углерода и урана (235U) бесконечной плоской размножающей гомогенной системы толщиной 20 см. Dс=0.85, sС = 3.4×10-3 барн, rС =1.6 г/см2
![]() Решение.
Решение.
![]() Поскольку k¥/(1+
Поскольку k¥/(1+ ![]() L2)=1 или k¥ = 1+
L2)=1 или k¥ = 1+![]() L2 и L2 = D/(åaU + åaC), а f= - доля нейтронов,
поглощенных ураном. В соотношении k¥ = hepf, в гомогенной среде e≈1 и p≈1, т.е.
L2 и L2 = D/(åaU + åaC), а f= - доля нейтронов,
поглощенных ураном. В соотношении k¥ = hepf, в гомогенной среде e≈1 и p≈1, т.е.
k¥ = hf =
h = 1+ ![]() , h=v×åf/åaU . Отсюда
=
, h=v×åf/åaU . Отсюда
= ![]() =
=![]()
или våf
-åaU=
åaC +![]() D.
(1)
D.
(1)
Рассчитаем макроскопическое сечение åaC = 1.6×6×1023×3.4×10-3×10-24 /12=2,72×10-4;
обозначим отношение NC/NU ≡ R, тогда åaU/åaC = saU /(RsaC) = 681/R×3.4×10-3 и åaU = 54.4/R, а åf/åaC = saU/(RsaC) и åf = åaC×sf /(RsaC) = 46,56/R; B2 = (p/a)2 = (p/21,7)2 .
Подставляем все в исходное уравнение (1) и решаем относительно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.