Основы физики реакторов. Деление ядер. Основные характеристики и параметры деления

Тогда количество этих нейтронов будет пропорционально объему этого сферического слоя dv = 4pR²vdt. Т.е.

Или имеем  . Обозначим k3v/Rº b, получим .

Среднее время пребывания нейтрона в шаре равно 1/b, и при k=0.3 составит t≈R/v.

Кстати, объем 1 т металлического шара урана равен 10⁶/18≈ 5.5×10⁴ см³, R≈23.5 см, следовательно, t≈23.5/10⁹ = 2.35×10^-8 с.

1.2.3      Критическая масса

Рассмотрим процесс в совокупности, т.е. в системе есть и рождение нейтронов и их утечка из объема.

                                                                                                                                                           (1.2.1)                         

Таким образом, изменение числа нейтронов в единицу времени будет определяться конкуренцией:

с одной стороны -  рождением нейтронов при делении нуклида [коэффициент а=(v -1)×N_я×s_а× v], т.е. физическими характеристиками размножающей среды, 

с другой - утечкой нейтронов из объема зоны деления (коэффициент b= k3v/R), т.е. геометрическими размерами объекта.

Соответственно а  можно связать с материальным, а b - с геометрическим параметрами.

Перепишем (1.1.1) как                , решение которого

                                                                                         n=n₀e^ct                                                               (1.2.2)

В соответствии со знаком коэффициента с возможны три состояния размножающей системы:

с>0:     a>b - рождений нейтронов больше, чем их утечка, т. е. количество нейтронов неограниченно возрастает с каждым циклом делений (система надкритична)

с<0:     a<b -  рождений нейтронов меньше, чем их утечка, т. е. количество нейтронов убывает (система подкритична)

с=0: самый интересный и информативный вариант 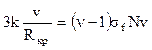   b = a     или                

отсюда   и

Таким образом,

при r>R_кр (или, что то же самое m>m_кр), b<b_кр  и  с>0 количество нейтронов экспоненциально возрастает, причем и при b=0.99b_кр и b=0.5b_кр , хотя и с разной скоростью;

при r<R_кр (или, что то же самое m<m_кр), b>b_кр  и  с<0 количество нейтронов через некоторое время обращается практически в нуль независимо от того имеем ли мы b=1.01b_кр или b=2b_кр.

1.2.4  Подкритическая и надкритическая массы при непрерывном источнике нейтронов

Пусть в начальный момент t=0 в размножающую систему поместили источник нейтронов мощностью q_o   

                                                                                                                    (1.2.3)                   

Ищем решение неоднородного уравнения как комбинацию частного решения однородного уравнения n^о и общего решения неоднородного j с начальным условием: n=0 при t=0. перепишем (1.2.3)

                                                                      n’-cn=q_o                                                                                                                             (1.2.4)

Решение n^о=e^ct однородного уравнения  n’-cn=0, комбинируем с j - j×e^ct  и подставляем в (1.2.4)

                                                    j’×e^ct  +сj×e^ct  - сj×e^ct  = q_o ,                                                              (1.2.5)

решение которого

                                                                                                                                                                     (1.2.6)

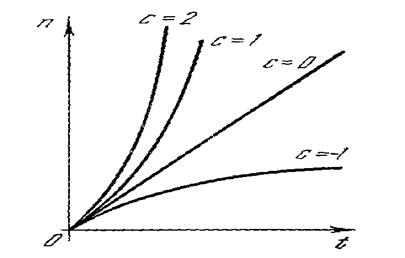
Проанализируем,  как меняется поток нейтронов в размножающей среде с непрерывным источником нейтронов для различных  значений с (см рисунок 1.1.2).

Из  уравнения (1.2.6) видно, что при достаточно большом t>> 1/|c| для  

с>0:  Величинасt>0, поэтому е^сt с ростом t становится гораздо больше 1 и                          , т.е. количество    нейтронов неограниченно возрастает (см рисунок 1.1.2, а)

с<0:  Величинасt<0, поэтому е^сt с ростом t становится гораздо меньше 1 и значение n приближается числу q₀/с ,т.е.   n≈q_o/c. И  чем меньше |с| (чем ближе к критическому состоянию), тем больше это постоянное значение. Таким образом, даже при очень слабом источнике (малом q_о) масса, близкая к критической может давать любое большое количество нейтронов, большое число делений, большое выделение энергии (см рисунок 1.1.2, в).

с=0: Обратимся к исходному дифференциальному уравнению dn/dt=q₀, решение которого дает n(t)=q₀t, т.е. количество нейтронов увеличивается пропорционально количеству времени нахождения источника  в размножающей среде (см рисунок 1.1.2, б)

Заключение

Основные положения, которые использованы при качественном рассмотрении критических параметров размножающей нейтроны среды:

− v скорость, а , следовательно, и энергия всех нейтронов постоянна и одинакова;

− на первой стадии процессы изменения количества нейтронов во времени (размножающая среда бесконечных размеров)  и в пространстве (среда ограниченных размеров