12.3 Получение обогащенного урана
Большинство реакторов работают на урановом топливе, в той или иной степени обогащенном по урану-235:
Низкое обогащение: 1 − 5%
Средняя степень обогащения : 8 − 20%
Высокая степень обогащения : более 20%
Обогащение урана осуществляется в физических процессах, скорость протекания которых различна для различных изотопов урана, и заключается в разделении исходного материала на две фракции (см. рис 12.3.1) бедненную (отвал) и обогащенную (продукт) по легкому или тяжелому изотопу.
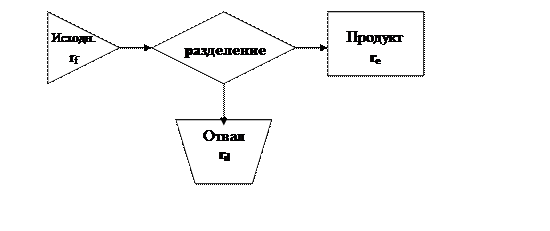
Рис 12.3.1 Принципиальная схема процесса обогащения
Критерием процесса обогащения является коэффициент разделения f или коэффициент обогащения α: пусть re − относительное содержание обогащаемого изотопа в обогащенной фракции, rd − относительное содержание обогащаемого изотопа в отвале, rf − относительное содержание обогащаемого изотопа в исходном продукте, для случая обогащения газообразного соединения (UF6) урана по урану -235
ri ≡ [235UF6]i /[238UF6]i ,
тогда
f=re/rd и α=re/rf .
12.3.1 Работа разделения
![]() Эффективность процесса обогащения урана определяется работой
разделения РР.
Эффективность процесса обогащения урана определяется работой
разделения РР.
Эта величина связана с разделительными потенциалами Ф, характеризующими единицу массы вещества с заданной концентрацией 23SU. Разделительный потенциал при концентрации с определяется выражением
(12.1)
Функция Фс выбрана так, чтобы разделительный потенциал был равен нулю, когда концентрация 23SU равна 0,5. Значение Фс увеличивается при увеличении или уменьшении с относительно значения 0,5. Поэтому, если разделять изотопы, находящиеся в веществе с одинаковыми концентрациями 235U и 238U, то вещество, прошедшее через разделительную установку, дает выход обогащенной и обедненной фракции с положительными значениями разделительного потенциала.
Предположим, что в качестве исходного (питающего) потока используется материал с массой М и концентрацией 235U, равной с, а на выходе установки масса обогащенного продукта с концентрацией с, равна Мр , а масса обедненного продукта с концентрацией cwравна Mw. Тогда работа разделения определяется увеличением в этом процессе величины, равной произведению массы на разделительный потенциал, т. е.
S = МрФр + МwФw - МФ.(12.2)
Поскольку Ф — величина безразмерная, то работа разделения измеряется в единицах массы1.
Сохранение полной массы в процессе разделения и сохранение в этом процессе массы 23SU дают два уравнения сохранения:
Мр + Mw= М, (12.3)
МрСр + Mwcw= Мс.(12.4)
Функция Ф выбрана таким образом, что работа разделения, которая затрачивается в разделительной установке," не зависит от концентраций изотопов в потоках питания, обогащения и отвала. Это показано на примере, рассмотренном ниже.
Пример 12.1. Обогатительный завод производит из естественного урана 400 т/год обогащенного урана с массовым содержанием 2%. Концентрация в отвале по массе составляет 0,25%. Какова разделительная мощность[1] Dзавода в тоннах в год? Сколько урана с 3%-ным обогащением может произвести такой же завод за год, если концентрация в отвале останется 0,25? Какой будет выход 3%-ного U, если обогащение в отвале увеличится до 0,35%?
Используя соотношение12.1 и замечая, что естественный уран содержит 0,711% 235U, вычисляем разделительные потенциалы обогащенного продукта, отвала и питания: Фр= 3,736; Фw= 5,959; Ф = 4,869.
Если масса отвала за год составляет Mw, то полная масса питания равна (Mw+ 400) т. Тогда из (12.4) имеем 400 . 0,02 + Mw.0,0025=(Mw + 400) . 0,00711, откуда Mw=1118 т/год, а полная масса питания М =1518 т/год. Следовательно, мощность разделения согласно (12.2) равна D = 400 . 3,736 +1118 . 5,959 - 1518 × 4,869 = 765 т/год.
Если концентрация обогащенного продукта увеличится до 3%, то Фр = = 3,2675. Подставляя это значение в (12.2) и (12.4), получаем
Мр .3,2675 + Mw.5,959 - (Мр + Mw) .4,869= 765 и
Мр .0,03 + Mw . 0,0025 = (Мр + Mw) . 0,00711. Решая эти уравнения, находим Мр = 201 т/год,
т. е. завод будет производить за год 3%-ного урана в 2 раза меньше
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.