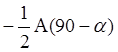Многоатомные молекулы. Приближение полного электронного спаривания. Роль энергии отталкивания, страница 3

.

Отсюда полная обменная энергия

          А(a) - 0.5А(90^O - a)                                                                           (9.8)

          Обобщая сказанное, можно сделать следующий вывод: в энергию произвольной системы электронов и ядер помимо энергии атомов Е_ат, составляющих систему, кулоновской энергии С_ij вносят свой вклад энергия спаренных электронов А_ij, энергия по неспаренным электронам А^*_ij (электроны из разных связей и поэтому их спины независимы), а также энергия по орбиталям с параллельными спинами А^**_ij.

Е = SЕ_ат + SС_ij + SА_ij - 0.5SА^*_ij - SА^**_ij .                                           (9.9)

Из выражения 9.9 видно, что максимальная энергия связи будет тогда, когда электроны, не принимающие участия в образовании ковалентной связи, будут отталкиваться друг от друга. Уравнение 9.9, соответствующее приближению полного спаривания, служит основой всей стереохимии. При его выводе было сделано ряд упрощений:

          - все АО связаны между собой попарно;

          - не учитываются все интегралы перекрывания S;

          - не учитываются все ионные и полярные составляющие;

          - учитываются только простые обменные интегралы.

Приближение полного спаривания в качественном отношении справедливо, но от него трудно ждать удовлетворительных количественных результатов (ошибка порядка 70 %).

          9.4. Молекула воды (метод ППЭС).

          Применение метода ППЭС проиллюстрируем на молекуле воды. Орбитали атомов водорода Н_а и Н_b образуют с орбиталями кислорода О(2р_х) и О(2р_y) углы a^* и a^** (см. рис.9.4). Такой схеме спаривания согласно уравнению 9.9 соответствует следующее выражение для обменной энергии:

Е_обм = + А(р_х;Н_а) + А(р_y;Н_b) - 0.5А(р_х;Н_b) - 0.5А(р_y;Н_а) -

 - 0.5 А(Н_a;Н_b) - 0.5 A(p_x;p_y).                                                                     (9.10)

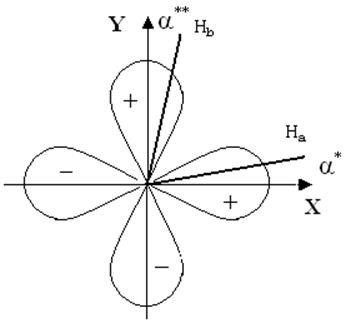
          Рис.9.4. Полное спаривание в молекуле Н₂О.

          В выражении 9.10 имеются два интеграла с коэффициентом + 1 (вклад электронов, участвующих в образовании ковалентных связей), четыре с коэффициентом - 1/2 (вклад непосредственно несвязанных электронов) и нет интегралов с коэффициентом - 1 (т.к. нет электронов со связанными параллельными спинами). Член A(p_x;p_y) равен нулю, т.к. орбитали p_x и p_y ортогоналены, член А(Н_a;Н_b) отвечает за отталкивание далеко стоящих друг от друга атомов водорода. Поэтому оба этих члена от угла не зависят. Из первых четырёх членов выражения 9.10 и выражения 9.7 вытекает, что энергия минимальна, когда a^* = a^** = 0^O, т.е. когда угол Н-О-Н равен 90^O. Применяя для кулоновской энергии (интеграл С) формулу, аналогичную 9.10, нетрудно показать, что кулоновская энергия не вносит вклада в эффекты, зависящие от направления. Выполненный анализ служит основой стереохимии двух р-связей; он позволяет объяснить и факт приближённого постоянства энергии связи. Теория, развитая для молекулы воды в равной мере применима для других молекул, имеющих не более, чем три р-электрона. Применима она и когда присоединённые атомы разные (с учётом принятых приближений). Важно отметить, что формулой, аналогичной 9.10, можно пользоваться для вычисления изменения энергии, когда углы a^* и a^** отклоняются от своих равновесных значений, что позволяет рассчитать частоту деформационных колебаний n. Для молекулы Н₂О расчёт даёт n = 1660 см^-1, а эксперимент - 1595 см^-1.

          9.5. Роль энергии отталкивания.