Многоатомные молекулы. Приближение полного электронного спаривания. Роль энергии отталкивания, страница 2

          - кулоновское отталкивание электронных облаков присоединённых атомов;

          - кулоновское и обменное отталкивание между связями типа О-Н;

          - участие (2s)²-электронов кислорода в образовании связи (гибридизация), что приводит к упрочнению связи и увеличению валентного угла;

          - некоторая вероятность других типов спаривания (кроме основного), приводящих к понижению энергию системы.

          9.3. Приближение полного электронного спаривания.

          После описания локализованных МО рассмотрим метод ВС в применении к многоатомным молекулам. Смысл локализации связи А-В в методе ВС заключается в том, что спаривание не зависит от других возможных спариваний в других частях молекулы. Как было установлено ранее для двухатомных молекул с одинаковыми ядрами значения энергии, соответствующие симметричной и антисимметричной волновым функциям, таковы:

Е_± = 2Е₀  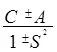+  .                                                                                (9.1)

Если молекула состоит из разных атомов, то 2Е_О = Е_А + Е_В. Пренебрегая интегралами S (он обычно мал) и С (для большинства молекул С » 0.15А, где А - обменный интеграл), получим:

Е_± = 2Е₀ ±  А.                                                                                        (9.2)

Энергия системы Е₊ соответствует синглету, а Е_- – триплету. Как указывалось ранее, синглету соответствует одна симметричная орбитальная волновая функция , умноженная на антисимметричную спиновую волновую функцию , а триплету три полных волновых функций, получаемых перемножением антисимметричной орбитальной волновой функции  на три типа симметричных спиновых волновых функций (a(1)a(2); a(1)b(2) + a(2)b(1); b(1)b(2)). Если спины принимают ориентацию совершенно случайно, то любая из указанных возможностей равновероятна. Следовательно, из 4 способов корреляции 3 приводят к антипараллельному, а 1 к параллельному расположению спинов. Поэтому средняя энергия взаимодействия

(+ А/4) + (- 3A/4) = - A/2.                                                                  (9.3)

Полученная энергия локальной связи в первом приближении определяется интегралом А -  обменным интегралом. Т.о. и в методе ВС решающую роль в образовании связи играет критерий максимального перекрывания волновых функций, участвующих в образовании связи.

          Используя метод ВС, рассмотрим подробнее угловую зависимость валентных связей на примере радикала ОН. Величина обменного интеграла будет зависеть от угла между связями

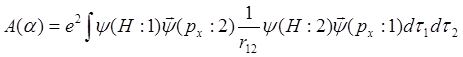.                             (9.4)

В соответствии со схемой, представленной на рис.9.3, векторный характер функции  позволяет представить её в виде:

.                                                            (9.5)

                                    H

                                                      р_e

                                  Xa O

                                                          р_h

          Рис.9.3. К вычислению обменного интеграла.

Подставляя 9.5 в 9.4, получим

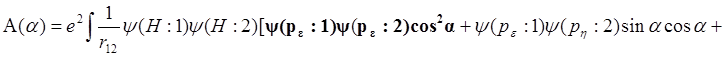
 .                           (9.6)

Первый из выделенных членов есть обменный интеграл с составляющей по линии О-Н; второй - с составляющей под углом 90^O к линии О-Н. Члены, содержащие sinacosa, исчезают в силу ортогональности y_ey_h. Поэтому получаем:

А(a) = А(0^O)×cos²a + А(90^O)sin²a.                                                   (9.7)

Соотношение 9.7 имеет большое значение. В конкретном случае радикала Н-О А(0^O) = - 2.0 эВ, А(90^O) = + 0.6 эВ. Следует отметить, что при спаривании орбиталей О(2р_х) и Н(1s) в величину обменной энергии вносит вклад не только А(a) от указанных орбиталей (хотя и основной), но и обменная энергия от орбитали О(2р_y). Значение последней будет равно