Расчет систематических и случайных ошибок автоматических устройств телекоммуникационных систем, страница 7

5.1.2. Исследование статической системы с линейно изменяющимся уровнем полезного сигнала.

Сформируем на входе системы линейно нарастающий во времени сигнал и визуально определим вид временной зависимости установившейся ошибки системы при значениях коэффициента усиления K_y = 1, K_y = 5, K_y = 10. Для этого будем использовать следующую схему:

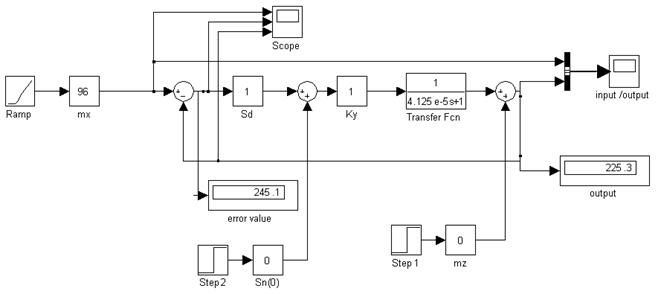
Рис. 18. Simulink – модель статической системы (полезный сигнал в виде линейно изменяющейся функции).

Результаты зафиксируем в виде осциллограмм, отражающих основные характерные особенности процессов (все в одном масштабе по оси времени 0 – 6e-4 с.):

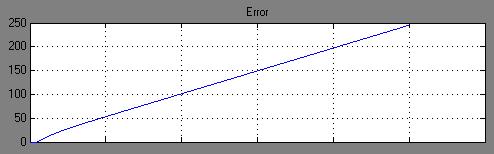
Рис. 19. Временная зависимость установившейся ошибки системы при значении коэффициента усиления K_y = 1.

Рис. 20. Временная зависимость установившейся ошибки системы при значении коэффициента усиления K_y = 5.

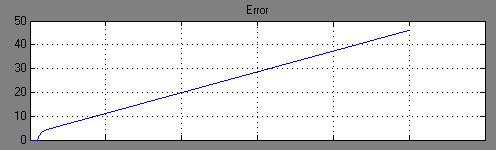
Рис. 21. Временная зависимость установившейся ошибки системы при значении коэффициента усиления K_y = 10.

5.1.3. Исследование статической системы с постоянным уровнем помехи.

Отключим входной полезный сигнал m_x (сделаем его равным нулю) и подадим в систему мешающее воздействие m_z в виде ступенчатой функции:

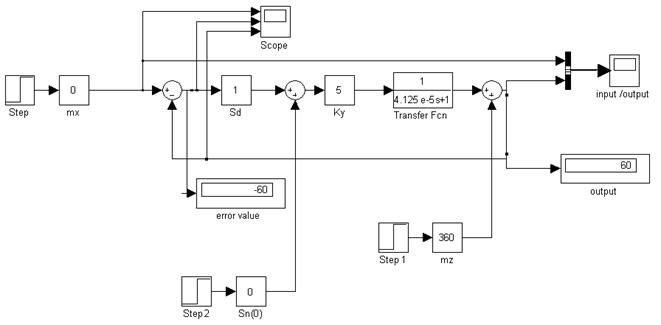
Рис. 22. Simulink – модель статической системы (помеха постоянного уровня).

Сформируем диаграммы входного воздействия, выходного сигнала, ошибки работы системы:

Рис. 23. Временные диаграммы входного воздействия, выходного сигнала, ошибки работы системы.

На основе собранной модели экспериментально определим количественную зависимость установившейся ошибки m_e работы системы от величины помехи m_z при нескольких значениях коэффициента усиления системы K_y. Результаты измерений занесем в таблицу:

Таблица 2. Ошибка m_e при воздействии помехи m_z.