Систематическая погрешность астатической системы при воздействии постоянной помехи отсутствует.
3. Расчет случайных погрешностей статической системы.
Случайная ошибка – ошибка, возникающая при воздействии на систему случайных процессов.
Мерой случайной ошибки будем считать ее дисперсию.
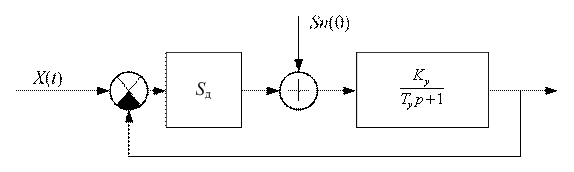
Рис. 9. Математическая модель статической системы для расчета случайной погрешности.
3.1. Случайная погрешность при воздействии сигнала (динамическая ошибка).
Расчет будем производить при отсутствии помехи в системе, т.е. Sn = 0.
Для нахождения ошибки необходимо вычислить коэффициент передачи системы от т.1 до т.2 (рис. 10).

Рис. 10. Математическая модель статической системы для расчета динамической ошибки.
Используя правило перемножения коэффициентов передачи при каскадном соединении, а также учитывая обратную связь, получим коэффициент передачи:
![]()
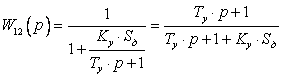

Запишем общую формулу для нахождения дисперсии динамической ошибки:
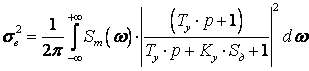 ,
,
где:
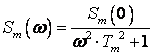 .
.
Преобразуем это выражение, используя правила действий с комплексными числами:


Этот интеграл является стандартным, решением которого является выражение:
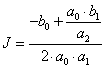 ,
,
где:

В итоге получаем:
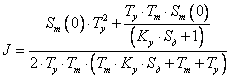
Подставляя численные значения, получаем:
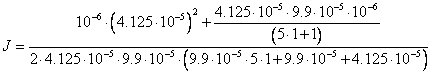 .
.
![]() .
.
Дисперсия динамической ошибки ![]() [В2].
[В2].
3.2. Случайная погрешность при воздействии помехи (флуктуационная ошибка).
Расчет будем производить при отсутствии сигнала в системе, т.е. Sm(ω) = 0.
Для нахождения ошибки необходимо вычислить коэффициент передачи системы от т.1 до т.2 (рис. 11).

Рис. 11. Математическая модель статической системы для расчета флуктуационной ошибки.
Используя правило перемножения коэффициентов передачи при каскадном соединении, а также учитывая обратную связь, получим коэффициент передачи:
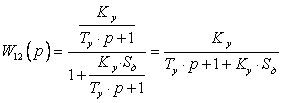 ,
,
 .
.
Запишем общую формулу для нахождения дисперсии флуктуационной ошибки:
 ,
,
где
![]() ;
;
Преобразуем это выражение, используя правила действий с комплексными числами.
 ;
;
Этот интеграл является стандартным, решением которого является выражение:
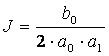 ,
,
где:

В итоге получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.