Составление математической модели задачи. Решение задачи линейного программирования графическим методом. Решение задачи симплекс-методом и с исполь­зованием компьютера (пакет Ехсеl), страница 6

Поэтому далее рассматриваем элементы  второй строки.

3. Находим .

Определим .

У второго поставщика осталось

 невывезенных единиц товаров.

В клетке  запишем 40.

Получаем таблицу:

Получим опорный план:

,

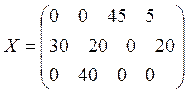который, приводит к затратам:

II. Проверим опорный план на оптимальность.

Запишем систему потенциалов для заполненных клеток. Для этого, перепишем предыдущую таблицу, дополнив ее величинами u_i и v_j.

1. По занятым клеткам опорного плана составим систему:

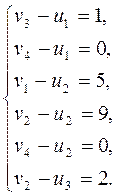
Система содержит 6 уравнения и 7 неизвестных. Положив, например, , найдем:

;

;

;

;

.

2. Для всех свободных клеток проверим выполнение условия . Имеем:

Клетка (1,1)                                                

Клетка (1,2)                                                

Клетка (2,3)                                                 

Клетка (3,1)                                                  .

Клетка (3,3)                                                  .

Клетка (3,4)                                                 .

План не оптимален. Условие не выполняется для клеток (1,1) и (1,2). Находим новый опорный план.

III. Переход к новому опорному плану:

1) выбираем одну из свободных клеток: либо (1,1), либо (1,2).

.

Так как  выбираем клетку (1,1).

2) строим для клетки (1,1) цикл пересчета:

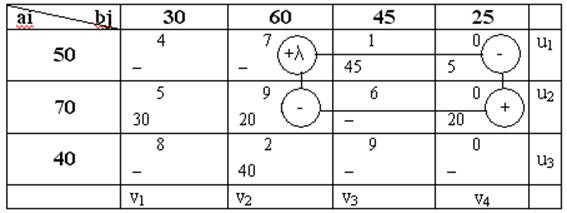
Находим  и переходим к новому опорному плану, перемещая по циклу величину .

Получаем новое опорное решение. Затраты уменьшились.

,

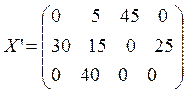3) проверяем опорное решение X’ на оптимальность:

Для занятых клеток опорного плана составим систему:

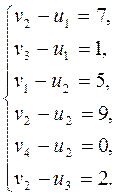
Решаем систему положив . Получаем:

;

;

;

.

Для всех свободных клеток проверим выполнение условия . Имеем:

Клетка (1,1)                                                

Клетка (1,4)                                             

Клетка (2,3)                                            

Клетка (3,1)                                                   .

Клетка (3,3)                                                  .

Клетка (3,4)                                              .

Так как для всех свободных клеток условия  выполняются, то данный опорный план является оптимальным.

Итак, получили оптимальное решение преобразованной ТЗ:

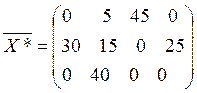, для которого оптимальные затраты на перевозки составят:

Возвращаясь к исходной открытой модели, видим, что ее оптимальное решение:

.

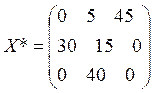Значения элементов последнего столбца матрицы  можно интерпретировать следующим образом: оптимальным является план, в котором у второго поставщика следует оставить 25 единиц товаров, у первого и третьего поставщиков – ничего не оставлять.

Ответ: ,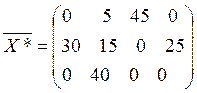

Задача 3.10

Задача 3а. Дана матрица С. Сделать содержательную поста­новку задачи о назначении, где значение целевой функции:

а) максимизируется,

б) минимизируется.

Составить математическую модель задачи о назначении с максимизацией целевой функции.

Решить обе задачи.

Задача 3б. Отбросив последний столбец матрицы С, сделать экономическую постановку задачи о назначении в случае мак­симизации и минимизации целевой функции. Составить матема­тическую модель задачи минимизации целевой функции.