Контрольная работа № 1. 3
Задача 1.10. 3
Задача 2.10. 5
Задача 3.10. 9
Контрольная работа № 2. 12
Задача 1.10. 12
Задача 2.10. 19
Задача 3.10. 25
Спивсок литературы.. 37
Составить математическую модель задачи.
На заготовительный участок поступили стальные прутья длиной 111 см. Необходимо разрезать их на заготовки 19, 23 и 30 см, которых требуется 311, 215 и 190 штук соответственно.
Построить модель, на основе которой сформулировать экстремальную задачу выбора варианта выполнения этой работы, при котором число разрезаемых прутьев минимально, если способы раскроя известны:
|
Способы раскроя прутьев |
Количество заготовок длины |
||
|
19 см |
23 см |
30 см |
|
|
I |
5 |
- |
- |
|
II |
4 |
- |
1 |
|
III |
3 |
1 |
1 |
|
IV |
1 |
- |
3 |
|
V |
2 |
- |
2 |
|
VI |
1 |
4 |
- |
|
VII |
- |
3 |
1 |
|
VIII |
- |
2 |
2 |
|
IX |
1 |
1 |
2 |
Решение
Из условия следует, что из прутьев длиной 111 см требуется нарезать заготовки:
по 19 см – 311 шт.
по 23 см – 215 шт.
по 30 см – 190 шт.
Количество прутьев каждого типа, которое получается при раскрое стального прута длиной 111 см по тому или иному способу раскроя, представлено в таблице.
Исходные данные задачи:
|
Заготовки |
Способ раскроя |
||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
|
|
1 типа (по 19 см) |
5 |
4 |
3 |
1 |
2 |
1 |
0 |
0 |
1 |
|
2 типа (по 23 см) |
0 |
0 |
1 |
0 |
0 |
4 |
3 |
2 |
1 |
|
3 типа (по 30 см) |
0 |
1 |
1 |
3 |
2 |
0 |
1 |
2 |
2 |
Требуется раскроить материал так, чтобы обеспечить минимальное число разрезаемых прутьев.
Обозначим через xi – количество стандартных заготовок, которые должны быть разрезаны по i-му варианту раскроя
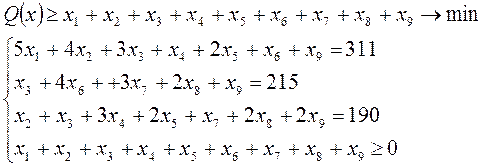
То есть для составления модели такой задачи необходимо задать типы раскроев, и из них просто выбрать оптимальный по числу используемых заготовок.
Решить задачу линейного программирования графическим методом:
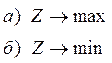
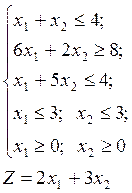
Решение
а) ![]()
Построим ОДР.
Областью решения линейного неравенства с двумя переменными является полуплоскость, лежащая по одну сторону от граничной прямой; уравнение этой прямой получится, если заменить знак неравенства знаком равенства.
Так, для первого неравенства уравнение граничной прямой имеет вид:
![]() .
.
Для построения прямой удобно привести уравнение к виду:
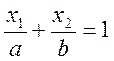 ,
,
где a и b – отрезки, отсекаемые соответственно на осях Ox1 и Ox2.
Имеем:
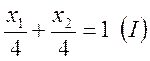 .
.
Для того чтобы определить расположение полуплоскости
относительно граничной прямой, подставим координаты какой-либо точки (например O(0;0))
в левую часть неравенства. Так как координаты точки удовлетворяют первому
неравенству (![]() ), то ОДР включает начало координат.
), то ОДР включает начало координат.
Поступая аналогично с остальными неравенствами, получим:
![]() либо
либо 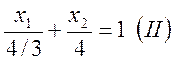 ;
;
![]() либо
либо 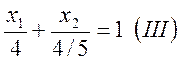 ;
;
![]() ;
;
![]() (ось Ox1);
(ось Ox1);
![]() (ось Ox2).
(ось Ox2).
Начало координат принадлежит области решений I (![]() ), III (
), III (![]() ) и IV (
) и IV (![]() ) неравенств; и не принадлежит области
решений II неравенства (
) неравенств; и не принадлежит области
решений II неравенства (![]() ).
).
Областью решений всех неравенств является общая область полуплоскостей, ограниченных граничными прямыми (I), (II), (III), (IV).
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат
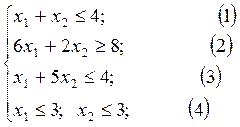
(1): 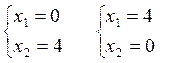 (2):
(2): 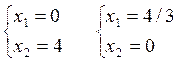
(3): 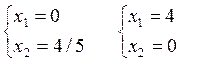 (4):
(4): 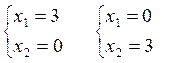
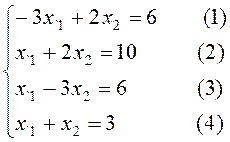
(1): 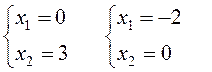 (2):
(2): 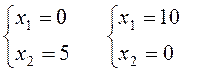
(3): 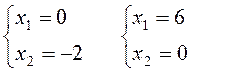 (4):
(4): 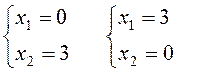
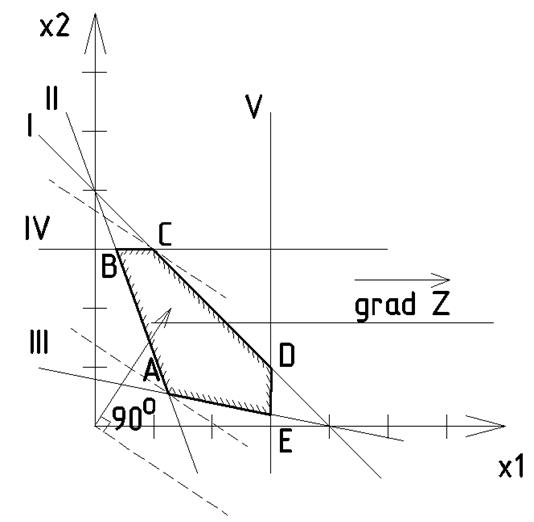
Рис. 1. ОЗЛП имеет единственное решение
Принимая во внимание условия неотрицательности
переменных (![]() ), получим в качестве ОДР заштрихованный
выпуклый многоугольник ABCDE.
), получим в качестве ОДР заштрихованный
выпуклый многоугольник ABCDE.
Далее обратимся к целевой функции ![]() . Выразим и построим в той же системе
координат вектор
. Выразим и построим в той же системе
координат вектор
![]() ,
, ![]()
и линию уровня, соответствующую значению Z = 0
(прямую, проходящую через начало координат перпендикулярно к вектору ![]() ). Перемещая линию уровня параллельно самой
себе в направлении вектора
). Перемещая линию уровня параллельно самой
себе в направлении вектора ![]() до тех пор, пока она
будет сохранять общие точки с ОДР, найдем, что в крайнем возможном положении
линия уровня пройдет через точку C. Этому положению и соответствует
до тех пор, пока она
будет сохранять общие точки с ОДР, найдем, что в крайнем возможном положении
линия уровня пройдет через точку C. Этому положению и соответствует ![]() .
.
Для нахождения координат точки C необходимо совместно решить систему уравнений граничных прямых (I) и (IV):
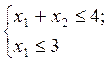
В результате получим: x1 = 3; x2 = 4/3.
Подставляя эти значения в целевую функцию, найдем ![]() .
.
б) ![]()
При нахождении Zmin
линию уровня будем перемещать параллельно самой себе в направлении вектора ![]() до первой точки, общей с областью
допустимых решений. В данном случае такой точкой является точка А.
до первой точки, общей с областью
допустимых решений. В данном случае такой точкой является точка А.
Для нахождения координат точки A необходимо совместно решить систему уравнений граничных прямых (II) и (III):
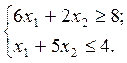
В результате получим: x1 = 8/7; x2 = 4/7.
Подставляя эти значения в целевую функцию, найдем 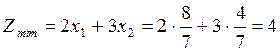 .
.
Ответ: а) X* = (3;4/3), Zmax = 14.
а) X* = (![]() ), Zmin
= 4.
), Zmin
= 4.
Решить задачу симплекс-методом и с использованием компьютера (пакет Ехсеl).
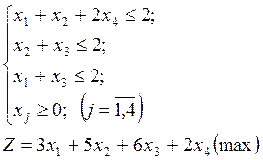
Решение
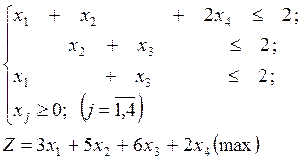
Необходимо перейти к минимизации целевой функции. Для
этого введем в рассмотрению функцию ![]() . Тогда
. Тогда ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.