Составление математической модели задачи. Решение задачи линейного программирования графическим методом. Решение задачи симплекс-методом и с исполь­зованием компьютера (пакет Ехсеl), страница 3

Теперь система приведена к базисному виду, базисными переменными являются x₁, x₃, x₄, свободной – x₂. Все свободные члены положительны, поэтому можем записать первоначальный опорный план:

.

Чтобы ответить, является ли он оптимальным, необходимо выполнить еще один шаг преобразований с разрешающим элементом a₄₂ = 2, чтобы выразить целевую функцию Z₁ только через свободную переменную x₃.

Получим новую таблицу:

Опорное решение , содержащееся в таблице, является оптимальным, так как вектор r = (0). Минимальное значение целевой функции  и, очевидно, .

Итак, , .

Ответ: , .

Контрольная работа № 2

Задача 1.10

Составить математическую модель транс­портной задачи и решить ее методом потенциалов.

В 2 пунктах отправления А и В находится соответст­венно 150 и 90 т горючего. Пункты № 1, 2, 3 требуют соответст­венно 60, 70, 110 т горючего. Стоимость перевозки 1 т горючего из пункта А в пункты № 1, 2, 3 соответственно равна 60, 10 и 40 р., а из пункта В – 12, 2 и 8 р. Составить оптимальный план перевозок горючего, чтобы общая сумма транспортных расходов была наименьшей.

Решить задачу, находя первоначальный опорный план:

а) методом минимального элемента;

б) методом северо-западного угла;

В каком случае оптимальное решение будет получено за меньшее количество шагов?

Решение

Пусть имеется m (А и Б) пунктов перевозок производства однородного продукта (горючего) и n (1, 2 и 3) пунктов потребления этого продукта. Мощности пунктов производства составляют   единиц, а потребности каждого j-го пункта потребления равны   единиц. Известны затраты  на перевозку единицы продукта от i-го поставщика j-му потребителю.

Пусть спрос и предложение совпадают, т.е. .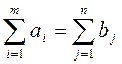

Так как данная задача является закрытой, предположим, что вся продукция от поставщиков будет вывезена, и спрос каждого из потребителей будет удовлетворен.

Составим математическую модель задачи. Обозначим через  количество продукта, перевозимого из i-го пункта производства в j-й пункт потребления. Тогда матрица:

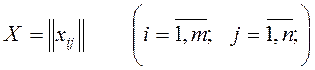 – план перевозок.

Матрицу 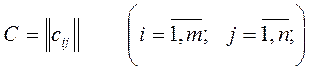 называют матрицей затрат (тарифов).

Внесем исходные данные и перевозки  в транспортную таблицу:

Обозначим искомые объемы перевозок от поставщиков к потребителям следующим образом:

x11 – объем перевозки от поставщика А к потребителю 1;

x12 – объем перевозки от поставщика А к потребителю 2;

x13 – объем перевозки от поставщика А к потребителю 3;

xа21 – объем перевозки от поставщика В к потребителю 1;

x22 – объем перевозки от поставщика В к потребителю 2;

x23 – объем перевозки от поставщика В к потребителю 3;

Составляем ограничения на запасы

для поставщика А:

для поставщика В:

Составляем ограничения на заказы

для потребителя 1:

для потребителя 2:

для потребителя 3:

Затраты на перевозку составят:

.

I. Метод нахождения северо-западного угла

Заметим, что 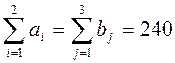, т.е. система ограничений совместна.