Составление математической модели задачи. Решение задачи линейного программирования графическим методом. Решение задачи симплекс-методом и с исполь­зованием компьютера (пакет Ехсеl), страница 2

Особенностью данной задачи является то, что система ограничений не приведена к базисному виду, нет разграничения переменных на базисные и свободные (есть только одна базисная переменная x₄). Поэтому прежде всего с помощью преобразований Жордана-Гаусса приведем систему к базисному виду. Для этого коэффициенты системы ограничений и целевой функции  занесем в таблицу:

Поиск ЗЛП состоит из следующих этапов: нахождения первоначального опорного плана, проверка полученного опорного плана на оптимальность и переход от одного опорного плана к другому, если найденный опорный план не является оптимальным.

Так как все свободные члены неотрицательны, то таблица содержит первоначальный опорный план. Его получим, положив свободные переменные равными нулю: x₁= x₂= x₃=0, при этом базисная переменная равны значениям соответствующих свободных членов. Следовательно:

Выпишем вектор r, компонентами которого являются коэффициенты при свободных переменных целевой функции:

.

Все компоненты вектора r отрицательны, следовательно, первоначальный опорный план  не является оптимальным.

За разрешающий столбец выберем любой столбец, содержащий хотя бы один положительный элемент, например первый.

Выбор разрешающей строки осуществим по тому же правилу, что при переходе от одного опорного решения к другому. Это правило гарантирует, что свободные члены новой таблицы останутся неотрицательными.

Имеем:

,

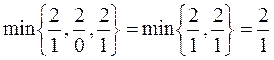т.е. за разрешающую строку примем первую (отмечена серым цветом) и за разрешающий элемент  a₁₁ = 1.

Выполнив шаг преобразований Жордана-Гаусса, приведем к таблице:

Система, записанная в данной таблице, разрешена относительно x₁ и x₄, но так как она содержит три уравнения, то необходимо ввести в базис еще одну переменную (x₂ или x₃) и при этом иметь в качестве разрешающей третью строку. Посмотрим, какой столбец с этой точки зрения следует брать за разрешающий столбец.

Если возьмем второй столбец, то за разрешающую строку следует выбрать первую или вторую строку, так как элемент в третьей строке отрицательный (неблагоприятный случай):

.

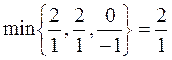Если же возьмем третий столбец, то за разрешающую строку следует выбрать третью строку (благоприятный вариант):

.

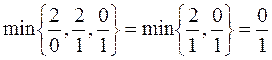Выберем третий столбец и, выполнив шаг преобразований Жордана-Гаусса с разрешающим элементом a₃₃ = 1, приведем к таблице: