Экономика и менеджмент \ Экономико-математические методы

Составление математической модели задачи. Решение задачи линейного программирования графическим методом. Решение задачи симплекс-методом и с использованием компьютера (пакет Ехсеl), страница 5

Клетка (2,1)

Клетка (2,2) .

План не оптимален. Условие не выполняется для клетки (2,1). Находим новый опорный план.

3. Переход к новому опорному плану:

1) выбираем свободную клетку (2,1).

2) строим для клетки (2,1) цикл пересчета:

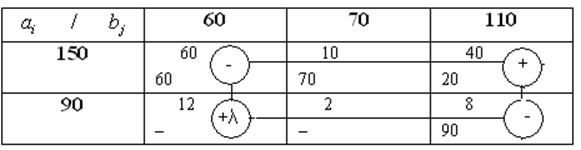
Находим и переходим к новому опорному плану, перемещая по циклу величину .

	60	70	110
150
90

Получаем новое опорное решение. Затраты уменьшились.

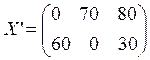3) проверяем опорное решение X’ на оптимальность:

Для занятых клеток опорного плана составим систему:

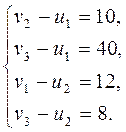
Решаем систему положив . Получаем:

;

Для всех свободных клеток проверим выполнение условия . Имеем:

Клетка (1,1)

Клетка (2,2)

Так как для всех свободных клеток условия выполняются, то данный опорный план является оптимальным.

Ответ: ,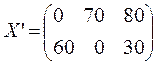

Задача 2.10

Сформулировать постановку и составить математическую модель транспортной задачи, условия которой приведены в таблице. Пояснить, с открытой или закрытой моделью имеем дело. Решить задачу методом потенциалов и дать содержательную интерпретацию оптимального решения.

ai bj	30	60	45
50	4	7	1
70	5	9	6
40	8	2	9

Решение

Исходные параметры модели транспортной задачи (ТЗ):

n – количество пунктов отправления;

m – количество пунктов назначения;

a_i – запас продукции в пункте отправления А_i (i =1,n) [ед. тов.].

b_j– спрос на продукцию в пункте назначения B_j (j =1,m) [ед.тов.].

c_ij – тариф (стоимость) перевозки единицы продукции из пункта отправления А_i в пункт назначения B_j [руб./ед.тов.].

Искомые параметры модели ТЗ:

x_ij – количество продукции, перевозимой из пункта отправления А_i в пункт назначения B_j [ед. тов.].

Z(X) – транспортные расходы на перевозку всей продукции [руб.].

Пусть имеется m пунктов перевозок производства однородного продукта и n пунктов потребления этого продукта. Мощности пунктов производства составляют единиц, а потребности каждого j-го пункта потребления равны единиц. Известны затраты на перевозку единицы продукта от i-го поставщика j-му потребителю.

Задача является закрытой, если спрос и предложение совпадают, т.е. .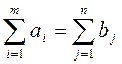

Проверим:

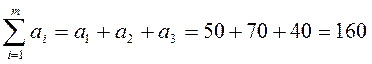
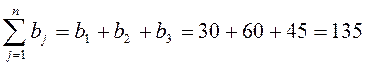Если равенство 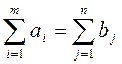не выполняется, либо запасы груза превышают потребности (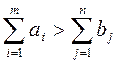), либо потребность в пунктах назначения превышает запас груза ().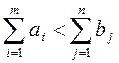

В нашем случае () объем ресурсов превышает потребность в них.

Соответствующую модель ТЗ называют открытой моделью.

Введем дополнительный «фиктивный» пункт назначения с объемом потребностей 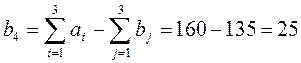и величинами транспортных издержек . И, получим, таким образом, закрытую модель ТЗ с тремя пунктами производства и четырьмя пунктами потребления.