Для кодирования символов кодом Хэмминга необходимо учитывать блочность данного кода, для этого разобьем ряд символов, полученных при кодировании источника, на блоки по четыре символа, и помножим каждый на матрицу G.
0101 1101 0011 0001 1010 0110 1110 0101 0110 0110 1110 0000 1011 0011 0100 0111 0101 0011 1100 1001
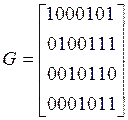
Кодовые слова в ней имеют структуру: С = ( х1, х2, х3, х4, с5, с6, с7 ), где
с5 = х1 + х2 + х3
с6 = х2 + х3 + х4
с7 = х1 + х2 + х4
(подразумевается сложение по модулю 2).
Реализовать такое кодирование можно при помощи устройства:
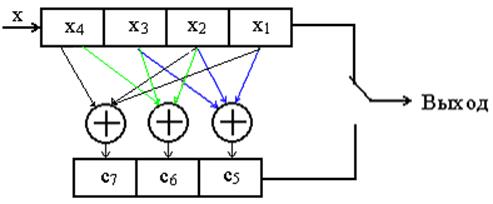
Рис. №14. Структура кодера для систематического (7,4) – кода.
Простым способом декодирования может быть в отбрасывании проверочных символов, но это не имеет смысла, т.к. не обеспечивало бы обнаружения и исправления ошибок. Для этого используют проверочную матрицу, состоящую из транспонированной паритетной матрицы (в свою очередь состоящую из элементов: с5, с6, с7 ) и добавочной в виде единичной матрицы
При умножении (по модулю два) вектор – строки, соответствующей принятой кодовой комбинации, слева на транспонированную проверочную матрицу НТ возможно два варианта матрицы синдрома:
1. Получение нулевого вектора. В этом случае символ передался без ошибки.
2. Получение вектора, схожего с одним из столбцов проверочной матрицы. В этом случае в символе, номер которого соответствует номеру этой строки, произошла ошибка.
Минус использования кода Хэмминга заключается в том, что он позволяет найти и исправить только одиночную ошибку, при двоичной ошибке произойдёт либо не обнаружение ошибки, либо указание на другой символ.
Построим код Хэмминга для нашей кодовой комбинации (стр. 9).
0101 1101 0011 0001 1010 0110 1110 0101 0110 0110 1110 0000 1011 0011 0100 0111 0101 0011 1100 1001
После разбиения на блоки, их можно представить в виде матрицы
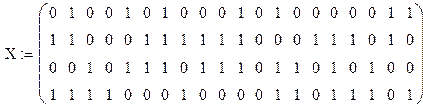
Транспонируем ее и помножим на порождающую матрицу G, получим:
,!!!!!!!
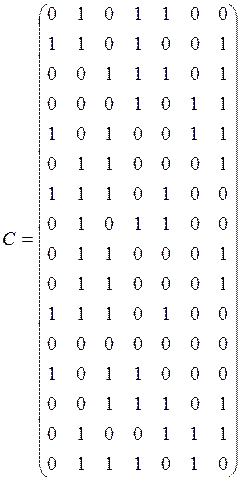тогда кодовую комбинацию модно записать в виде:
0101100 1101001 0011101 0001011 1010011 0110001 1110100 0101100 0110001 0110001 1110100 0000000 1011000 0011101 0100111 0111010
Исходное выражение «Всеимбаденадеждапорока» в коде Хемминга будет выглядеть так:
010111011111100011010011011100101011001101110000010110011010001110101001111001001
0101100110100100111010001011101001101100011110100010110001100010110001111010000000001011000001110101001110111010
Расчет вероятности двукратной ошибки в пределах одного кодового слова.
Требуется рассчитать вероятность искажения двух разрядов в одном кодовом слове. Рассмотрим задачу так: рассчитаем вероятность принятия 0011 при передаче 1111.
р01 и р10- вероятности принятия «1» за «0» и наоборот.
(1-р01) и (1- р10)- вероятности правильного приема «0» и «1»
событие D = (принята комбинация 0111)
Требуется рассчитать условную вероятность р(D/Н1).
р(D/Н1) = р(0111/Н1) = р(0|H1)×р(0|Н1)×р(1|Н1)×р(1|Н1) - при условии, что символы искажаются независимо друг от друга.
р(1/Н1) = (1-р10) и р(0/Н1) = р10 ,то
р(D/Н1) = р102(1-р10)2 = 2.2×10-4.
Как видно, вероятность ошибки одновременно в двух разрядах кодового слова очень мала.
Заключение
В процессе выполнения работы произведено кодирование дискретного сообщения с целью сократить избыточность источника для повышения скорости передачи, введение дополнительной избыточности канальным кодированием для помехоустойчивости, а также осуществлен прием сообщения.
Выяснилось, что при отношении сигнал/шум ≤ 0.45 применение некогерентного приема невозможно; что в канале с сильными помехами приеме скорость передачи информации значительно падает по сравнению с каналом без помех; что вероятность ошибки одновременно в двух разрядах кодового слова, кодированного по Хеммингу, очень мала.
.
Список литературы.
1. Введение в теорию электрической связи. Учебное пособие. В.Н. Васюков, 2003 г.
2. Теория электрической связи. Учебник для вузов / А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк.—2-е изд., перераб. и доп.—М.: Радио и связь, 1986
3. Баскаков С.И. Радиотехнические цепи и сигналы: – М.: Высш. шк., 1988
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.